Центральная предельная теорема: различия между версиями
Patarakin (обсуждение | вклад) Нет описания правки |
Patarakin (обсуждение | вклад) |
||
| (не показано 10 промежуточных версий этого же участника) | |||
| Строка 2: | Строка 2: | ||
|Description=Центра́льные преде́льные теоре́мы (ЦПТ) — класс теорем в теории вероятностей, утверждающих, что сумма достаточно большого количества слабо зависимых случайных величин, имеющих примерно одинаковые масштабы (ни одно из слагаемых не доминирует, не вносит в сумму определяющего вклада), имеет распределение, близкое к нормальному. Так как многие случайные величины в приложениях формируются под влиянием нескольких слабо зависимых случайных факторов, их распределение считают нормальным. При этом должно соблюдаться условие, что ни один из факторов не является доминирующим. Центральные предельные теоремы в этих случаях обосновывают применение нормального распределения. | |Description=Центра́льные преде́льные теоре́мы (ЦПТ) — класс теорем в теории вероятностей, утверждающих, что сумма достаточно большого количества слабо зависимых случайных величин, имеющих примерно одинаковые масштабы (ни одно из слагаемых не доминирует, не вносит в сумму определяющего вклада), имеет распределение, близкое к нормальному. Так как многие случайные величины в приложениях формируются под влиянием нескольких слабо зависимых случайных факторов, их распределение считают нормальным. При этом должно соблюдаться условие, что ни один из факторов не является доминирующим. Центральные предельные теоремы в этих случаях обосновывают применение нормального распределения. | ||
|Field_of_knowledge=Математика | |Field_of_knowledge=Математика | ||
|similar_concepts=дисперсия, математическое ожидание | |||
|Environment=NetLogo, StarLogo Nova, R | |Environment=NetLogo, StarLogo Nova, R | ||
}} | }} | ||
https://upload.wikimedia.org/wikipedia/commons/thumb/7/7b/IllustrationCentralTheorem.png/600px-IllustrationCentralTheorem.png | https://upload.wikimedia.org/wikipedia/commons/thumb/7/7b/IllustrationCentralTheorem.png/600px-IllustrationCentralTheorem.png | ||
== Классическая ЦПТ == | == Классическая ЦПТ == | ||
Пусть <math>X_1,\ldots, X_n</math> есть последовательность независимых одинаково распределённых случайных величин, имеющих конечные [[математическое ожидание]] <math>\mu</math> и [[Дисперсия | Пусть <math>X_1,\ldots, X_n</math> есть последовательность независимых одинаково распределённых случайных величин, имеющих конечные [[математическое ожидание]] <math>\mu</math> и [[Дисперсия|дисперсию]] <math>\sigma^2</math>. Пусть также | ||
: <math>S_n = \sum\limits_{i=1}^n X_i</math>. | : <math>S_n = \sum\limits_{i=1}^n X_i</math>. | ||
Тогда | Тогда | ||
| Строка 16: | Строка 16: | ||
можно переписать результат центральной предельной теоремы в следующем виде: | можно переписать результат центральной предельной теоремы в следующем виде: | ||
: <math>\sqrt{n} \frac{ \bar{X}_n - \mu}{\sigma} \to N(0,1)</math> [[Сходимость по распределению|по распределению]] при <math>n \to \infty</math>. | : <math>\sqrt{n} \frac{ \bar{X}_n - \mu}{\sigma} \to N(0,1)</math> [[Сходимость по распределению|по распределению]] при <math>n \to \infty</math>. | ||
'''Классическая формулировка:''' | |||
Пусть <math>X_1, X_2, ..., X_n</math> — независимые одинаково распределённые случайные величины с конечными <math>M(X_i) = \mu</math> и <math>D(X_i) = \sigma^2</math>. Тогда: | |||
<math>\frac{\bar{X}_n - \mu}{\sigma/\sqrt{n}} \xrightarrow{d} N(0, 1)</math> | |||
при <math>n \to \infty</math>, где <math>\bar{X}_n = \frac{1}{n}\sum_{i=1}^{n} X_i</math> — выборочное среднее. | |||
== Интерактивное представление центральной предельной теоремы == | |||
* https://gallery.shinyapps.io/CLT_mean/ | |||
{{#widget:iframe | |||
|url=https://gallery.shinyapps.io/CLT_mean/ | |||
|width=1000 | |||
|height=800 | |||
}} | |||
== Модель [[Central Limit Theorem]] == | |||
{{#ask: [[Central Limit Theorem]] | ?Description }} | |||
<netlogo model="CentralLimitTheorem" /> | |||
Текущая версия от 21:47, 8 января 2026
| Описание | Центра́льные преде́льные теоре́мы (ЦПТ) — класс теорем в теории вероятностей, утверждающих, что сумма достаточно большого количества слабо зависимых случайных величин, имеющих примерно одинаковые масштабы (ни одно из слагаемых не доминирует, не вносит в сумму определяющего вклада), имеет распределение, близкое к нормальному. Так как многие случайные величины в приложениях формируются под влиянием нескольких слабо зависимых случайных факторов, их распределение считают нормальным. При этом должно соблюдаться условие, что ни один из факторов не является доминирующим. Центральные предельные теоремы в этих случаях обосновывают применение нормального распределения. |
|---|---|
| Область знаний | Математика |
| Авторы | |
| Поясняющее видео | |
| Близкие понятия | Дисперсия, Математическое ожидание |
| Среды и средства для освоения понятия | NetLogo, StarLogo Nova, R |
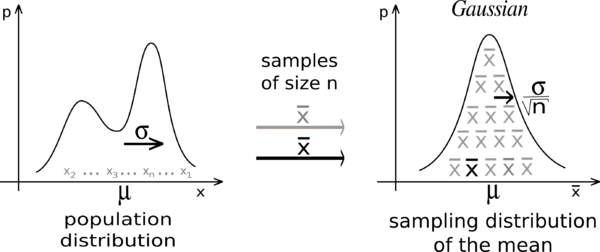
Классическая ЦПТ
Пусть [math]\displaystyle{ X_1,\ldots, X_n }[/math] есть последовательность независимых одинаково распределённых случайных величин, имеющих конечные математическое ожидание [math]\displaystyle{ \mu }[/math] и дисперсию [math]\displaystyle{ \sigma^2 }[/math]. Пусть также
- [math]\displaystyle{ S_n = \sum\limits_{i=1}^n X_i }[/math].
Тогда
- [math]\displaystyle{ \frac{S_n - \mu n}{\sigma \sqrt n} \to N(0,1) }[/math] по распределению при [math]\displaystyle{ n \to \infty }[/math],
где [math]\displaystyle{ N(0,1) }[/math] — нормальное распределение с нулевым математическим ожиданием и стандартным отклонением, равным единице. Определяя выборочное среднее первых [math]\displaystyle{ n }[/math] величин как
- [math]\displaystyle{ \bar{X}_n = \frac{1}{n} \sum\limits_{i=1}^n X_i }[/math],
можно переписать результат центральной предельной теоремы в следующем виде:
- [math]\displaystyle{ \sqrt{n} \frac{ \bar{X}_n - \mu}{\sigma} \to N(0,1) }[/math] по распределению при [math]\displaystyle{ n \to \infty }[/math].
Классическая формулировка:
Пусть [math]\displaystyle{ X_1, X_2, ..., X_n }[/math] — независимые одинаково распределённые случайные величины с конечными [math]\displaystyle{ M(X_i) = \mu }[/math] и [math]\displaystyle{ D(X_i) = \sigma^2 }[/math]. Тогда:
[math]\displaystyle{ \frac{\bar{X}_n - \mu}{\sigma/\sqrt{n}} \xrightarrow{d} N(0, 1) }[/math]
при [math]\displaystyle{ n \to \infty }[/math], где [math]\displaystyle{ \bar{X}_n = \frac{1}{n}\sum_{i=1}^{n} X_i }[/math] — выборочное среднее.
Интерактивное представление центральной предельной теоремы
Модель Central Limit Theorem
| Description | |
|---|---|
| Central Limit Theorem | Модель "Central Limit Theorem" представляет население, распределённое по некоторой переменной (например, общие активы в тысячах долларов). Население распределено произвольно — не обязательно нормально — но выборочные средние из этой популяции тем не менее накапливаются в распределении, которое приближается к нормальной кривой. |
