Категория:Model: различия между версиями
Patarakin (обсуждение | вклад) |
Patarakin (обсуждение | вклад) |
||
| (не показаны 3 промежуточные версии этого же участника) | |||
| Строка 1: | Строка 1: | ||
{{#default_form:Model}} | '''{{#default_form:Model}}''' | ||
Категория, в которой собраны (многоагентные) модели и их описание. | Категория, в которой собраны (многоагентные) модели и их описание. | ||
== Категория Model содержит {{#ask: [[Категория:Model]] [[Description::+]] | format = count }} объектов == | |||
=== StarLogo Nova === | |||
{{#ask: [[Категория:Model]] [[Environment::StarLogo Nova]]| ?Description | ?Environment}} | |||
---- | |||
{{#ask: [[Категория:Model]] | ?Description | ?Environment}} | {{#ask: [[Категория:Model]] | ?Description | ?Environment}} | ||
Версия 09:56, 27 апреля 2024
Эта категория использует форму Model. Категория, в которой собраны (многоагентные) модели и их описание.
Категория Model содержит 38 объектов
StarLogo Nova
| Description | Environment | |
|---|---|---|
| Air Pollution - Buses and Cars | Когда модель работает, автобусы непрерывно следуют по дороге. В домах есть люди, которым нужно добираться на работу. Если автобус проезжает мимо дома, человек из этого дома «садится в автобус». Однако, если автобус не прибудет достаточно скоро, вместо этого человек использует личную машину, в результате чего на дороге появится машина, которой необходимо проехать определенное расстояние, прежде чем ее уберут с дороги. Автомобили выбрасывают 1 загрязнение каждые 7 «тиков». Автобусы выбрасывают одно загрязнение каждые 1 тик. Автомобили и автобусы следуют основным правилам дорожного движения: снижайте скорость, если многолюдно, и останавливайтесь, если впереди нет места для движения.
| StarLogo Nova |
| Flocking (model) | Модель самопроизвольного формирования стаи в результате действий множества участников (птиц, рыб, людей). Модель формирования стаи - это классическая агентно-ориентированная модель, основанная на оригинальных моделях Рейнольдса (1987). Модель демонстрирует, что стаи птиц могут возникать даже в отсутствии специальных птиц-вожаков, которые ведут всех за собой. Скорее, каждая птица следует общему же набору правил, и из выполнения всеми простых правил появляются стаи. Каждая птица следует трем правилам: «выравнивание», «разделение» и «сплоченность».
Правило «разделения» имеет приоритет над двумя другими, что означает, что если две птицы приближаются друг к другу, они всегда будут разделяться. В этом случае два других правила отменяются до тех пор, пока не будет достигнуто минимальное разделение. Эти три правила влияют только на направление птицы. Каждая птица всегда движется вперед с одинаковой постоянной скоростью. Правила удивительно надежны и могут быть адаптированы к скоплению насекомых, стаям рыб и паттернам «V» стаи гусей (Stonedahl & Wilensky, 2010a). | NetLogo StarLogo Nova Scratch Snap! |
| Giraffe collecting coins | Кто-то рассыпал много монет на улице. Жираф это увидел, и пошёл их собирать. | StarLogo Nova |
| Great white shark | Четыре большие белые акулы проголодались и вышли на охоту. Обнаружив косяк рыб, они мигом расправляются с ним, съев всех рыб до последней. За происходящим наблюдает ихтиолог и ведет подсчет съеденных рыб акулами за время охоты, для наглядности он составил график.
| StarLogo Nova |
| Hungry raccoon | Мама Енот выходит на лужайку в поисках морковки, чтобы накормить 100 детей. В ходе своей вылазки мама Енот ведет счет морковок, чтобы дети точно наелись.
 | StarLogo Nova |
| Leaders & Followers (model) | Модель лидеров (харизматиков) и их последователей - тех, кто за ними следует и устанавливает с ними связи.
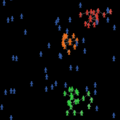 | NetLogo StarLogo Nova |
| Segregation (model) | Модель сегрегации
| NetLogo StarLogo Nova |
| The princess is collecting coins and planting flowers near her castle. | Принцесса около своего замка находит и собирает монетки, которые оставили туристы, чтобы вернуться, и на эти деньги украшает территорию, сажая разные цветочки.
| StarLogo Nova |
| This is my fish! | Посмотрим, кто из нас действительно голоден! Пингвины пытаются забрать и съесть всю возможную рыбу. | StarLogo Nova |
| Traffic jams | Модель формирования и рассасывания дорожной пробки, реализованная в нескольких средах многоагентного моделирования | NetLogo StarLogo Nova Snap! |
| Модель Лотки — Вольтерры | Моде́ль Ло́тки — Вольте́рры (модель Ло́тки — Вольтерра́) — модель взаимодействия двух видов типа «хищник — жертва», названная в честь своих авторов (Лотка, 1925; Вольтерра 1926), которые предложили модельные уравнения независимо друг от друга. | StarLogo Nova R Netlogo |
| Насосы и испарение | Модель физических процессов, в которой происходит испарение воды | StarLogo Nova |
| Охота морских коньков | Модель, которая показывает, каким образом увеличивается морской конек относительно того, сколько рыбы ему удастся съесть. | StarLogo Nova |
| Поезд и рыбы | На город, в котором царят только мирные взаимоотношения между женщинами и лягушками, нападают танки, замаскировавшись под поезд. Что происходит дальше? | StarLogo Nova |
| Собирание учеников в классы | 3 Учителя - черный, красный и желтый собирают учеников в свои классы | StarLogo Nova |
| Термиты | Модель термитника (муравейника), когда тупые, слабые и слабовидящие агенты перемещаются по полю и собирают на нём палочки. Есть версия "Термиты с журналом", когда все действия термитов над палочками записываются в лог-файл и потом можно построить графы команд, где в команду объединены термиты, носившие одни и те же палочки. | NetLogo StarLogo Nova |
| Футбольное поле с множеством мячиков | Модель сбора данных с поля, на котором множество игроков взаимодействуют со множеством мячиков. Модель используется для
| StarLogo Nova |
| Description | Environment | |
|---|---|---|
| Air Pollution - Buses and Cars | Когда модель работает, автобусы непрерывно следуют по дороге. В домах есть люди, которым нужно добираться на работу. Если автобус проезжает мимо дома, человек из этого дома «садится в автобус». Однако, если автобус не прибудет достаточно скоро, вместо этого человек использует личную машину, в результате чего на дороге появится машина, которой необходимо проехать определенное расстояние, прежде чем ее уберут с дороги. Автомобили выбрасывают 1 загрязнение каждые 7 «тиков». Автобусы выбрасывают одно загрязнение каждые 1 тик. Автомобили и автобусы следуют основным правилам дорожного движения: снижайте скорость, если многолюдно, и останавливайтесь, если впереди нет места для движения.
| StarLogo Nova |
| Artificial Anasazi | Проект был посвящен воспроизведению древнеиндейской культуры анасази в виде цифрового искусственного общества. Была смоделирована динамика города Кайента (Аризона, США) в период с 900 по 1350 год нашей эры, после которого упомянутая цивилизация исчезла. Главный вопрос для археологов был следующий: почему так произошло? С использованием расширенной версии модели Sugarscape была создана окружающая агентов среда с учетом гидрологических особенностей территории, плодородности почвы, засушливости и других параметров. В свою очередь, расселение анасази по территории в рамках цифровой модели осуществлялось на основе данных, собранных лабораторией годичных колец Аризонского университета (Tree Ring Laboratory at the University of Arizona). Each agent represents a household of five persons. Each household makes annual decisions on where to farm and where to settle. A household has an age, and a stock of food surplus previous years. Each cell represents a 100 meter by 100 meter space. Each cell is within one of the different zones of land: General Valley Floor, North Valley Floor, Midvalley Floor, Arable Uplands, Uplands Non-Arable, Kinbiko Canyon or Dunes. These zones have agricultural productivity that is determined by the Palmer Drought Severity Index (PDSI). | NetLogo |
| Basketball analytics | Drafting agent-based modeling into basketball analytics
| NetLogo |
| Bears | Bears walk and eat the growing grass | Slnova |
| Butterfly model | Эксперименты с моделью приведены в книге Agent-Based and Individual-Based Modeling: A Practical Introduction | NetLogo |
| Dawkins Weasel | Dawkins Weasel is a NetLogo model that illustrates the principle of evolution by natural selection. It is inspired by a thought experiment presented by Richard Dawkins in his book The Blind Watchmaker (1986). He presents the idea as follows: | NetLogo |
| Fire (model) |
 Запустите модель Fire несколько раз. Если мы запустим его с низкой плотностью деревьев, мы увидим, как и ожидалось, очень небольшое распространение огня. Если мы запустим его с очень высокой плотностью деревьев, мы, как и ожидалось, увидим, как лес уничтожается неумолимым маршем огня. Чего ожидать при средней плотности? Многие предполагают, что если плотность установлена на 50 процентов, то вероятность того, что огонь достигнет правого края леса, будет 50 процентов. Однако если мы попробуем это сделать, то увидим, что при 50-процентной плотности огонь не распространяется сильно. Если мы увеличим его до 57 процентов, огонь горит больше, но обычно все равно не достигает другой стороны леса. Однако если мы увеличим плотность до 61 процента, то есть всего на 2 процента больше, огонь неизбежно достигнет другой стороны. Это неожиданно. Мы ожидаем, что небольшое изменение плотности окажет относительно небольшое влияние на распространение огня. Но, как выясняется, модель Fire имеет «критический параметр» 59% плотности. | NetLogo |
| Fireflies (model) | Модель синхронизации мигания светлячков
По ночам самцы светлячков Photinus carolinus мигают для привлечения самок. При этом вспышки отдельной особи не периодичны. Но если несколько насекомых оказываются рядом, они начинают мигать синхронно. Несколько ярких вспышек в течение пары секунд повторяются через более длительные промежутки времени. Координироваться светлячкам помогает зрение: наблюдая за миганием других особей, они начинают подстраиваться под их ритм.
| NetLogo |
| Flocking (model) | Модель самопроизвольного формирования стаи в результате действий множества участников (птиц, рыб, людей). Модель формирования стаи - это классическая агентно-ориентированная модель, основанная на оригинальных моделях Рейнольдса (1987). Модель демонстрирует, что стаи птиц могут возникать даже в отсутствии специальных птиц-вожаков, которые ведут всех за собой. Скорее, каждая птица следует общему же набору правил, и из выполнения всеми простых правил появляются стаи. Каждая птица следует трем правилам: «выравнивание», «разделение» и «сплоченность».
Правило «разделения» имеет приоритет над двумя другими, что означает, что если две птицы приближаются друг к другу, они всегда будут разделяться. В этом случае два других правила отменяются до тех пор, пока не будет достигнуто минимальное разделение. Эти три правила влияют только на направление птицы. Каждая птица всегда движется вперед с одинаковой постоянной скоростью. Правила удивительно надежны и могут быть адаптированы к скоплению насекомых, стаям рыб и паттернам «V» стаи гусей (Stonedahl & Wilensky, 2010a). | NetLogo StarLogo Nova Scratch Snap! |
| Giraffe collecting coins | Кто-то рассыпал много монет на улице. Жираф это увидел, и пошёл их собирать. | StarLogo Nova |
| Great white shark | Четыре большие белые акулы проголодались и вышли на охоту. Обнаружив косяк рыб, они мигом расправляются с ним, съев всех рыб до последней. За происходящим наблюдает ихтиолог и ведет подсчет съеденных рыб акулами за время охоты, для наглядности он составил график.
| StarLogo Nova |
| Hungry raccoon | Мама Енот выходит на лужайку в поисках морковки, чтобы накормить 100 детей. В ходе своей вылазки мама Енот ведет счет морковок, чтобы дети точно наелись.
 | StarLogo Nova |
| Leaders & Followers (model) | Модель лидеров (харизматиков) и их последователей - тех, кто за ними следует и устанавливает с ними связи.
 | NetLogo StarLogo Nova |
| Life (model) | Модель игры в жизнь. This particular cellular automaton is called The Game of Life. A cellular automaton is a computational machine that performs actions based on certain rules. It can be thought of as a board which is divided into cells (such as square cells of a checkerboard). Each cell can be either "alive" or "dead." This is called the "state" of the cell. According to specified rules, each cell will be alive or dead at the next time step. | NetLogo |
| Multi-mediator model | Модель позволяет проводить вычислительные эксперименты по изучению математических идей учениками средней школы. Модель посвящена проблема низкой успеваемости по математике у студентов с низким социально-экономическим статусом (SES). В Австралии 15-летние студенты с низким SES отстают на три года по уровню математической подготовки. Подобная же ситуация наблюдается и в США. Цель исследования - исследовать, может ли компьютерное моделирование помочь улучшить математическую успеваемость студентов с низким SES, чтобы преодолеть трехлетнее отставание. | NetLogo |
| Piaget-Vygotsky (model) | Модель «обучения через игру» была создана для следующих целей:
| NetLogo |
| Preferential Attachment | Модель предпочтительного присоединения - Preferential Attachment - Процесс предпочтительного присоединения - это любой из классов процессов, в которых некоторое количество, обычно некоторое форма богатства или кредита распределяется между несколькими людьми или объектами в зависимости от того, сколько они уже имеют, так что те, кто уже богат, получают больше, чем те, кто не богат. «Предпочтительная привязанность» - это лишь последнее из многих названий, которые были даны таким процессам. Они также упоминаются как «богатые становятся богаче». Процесс предпочтительного присоединения генерирует распределение «с длинным хвостом » после распределения Парето или степенной закон в его хвосте. Это основная причина исторического интереса к предпочтительной привязанности: распределение видов и многие другие явления наблюдаются эмпирически, следуя степенным законам, и процесс предпочтительной привязанности является ведущим механизмом для объяснения этого поведения. Предпочтительное прикрепление считается возможным основанием для распределения размеров городов, богатства чрезвычайно богатых людей, количества цитирований, полученных научными публикациями, и количества ссылок на страницы во всемирной паутине.
 | NetLogo |
| Prisoner's dilemma | Дилемма заключенного - это классическая задача в теории игр, которую можно использовать для преподавания вычислительной истории, иллюстрируя динамику сотрудничества и конкуренции в исторических контекстах. Дилемма заключенного может быть включена в вычислительную историю несколькими способами: 1) Моделирование исторических взаимодействий: Дилемма заключенного может быть использована в качестве основы для моделирования взаимодействия между историческими акторами, такими как отдельные люди, группы или государства. Моделируя решения и выплаты этих субъектов в различных сценариях, учащиеся могут получить представление о факторах, повлиявших на сотрудничество или конкуренцию в исторических событиях. 2) Изучение возникновения норм и институтов: Дилемма заключенного может быть использована для изучения возникновения социальных норм и институтов в исторических обществах. Например, учащиеся могут создать агентные модели, которые имитируют взаимодействие людей, следующих правилам дилеммы заключенного, а затем проанализировать, как различные стратегии, такие как tit-for-tat (око за око) или "всегда сотрудничать", приводят к развитию норм сотрудничества или к его разрушению. | NetLogo |
| School Choice ABM | Модель "School Enrollment" представляет собой пространственно-эксплицитную вычислительную модель, которая иллюстрирует систему школьного образования в Чили, основанную на рыночных принципах. В этой модели студенты могут выбирать между различными типами школ: государственными, частными с ваучерами и частными платными. Модель изображает город, в котором расположены школы и студенты.
Есть версии, когда имеют дополнительные атрибуты, такие как географическое положение, сектор (государственная или частная), стоимость обучения, уровень достижений студентов, максимальная вместимость, год открытия и закрытия, а также вероятность того, что о ней узнают ученики. | NetLogo |
| Segregation (model) | Модель сегрегации
| NetLogo StarLogo Nova |
| Slime (агрегация слизевиков) | Эта модель показывает, как существа могут объединяться в кластеры без контроля со стороны клетки-лидера или пейсмейкера. Это открытие было впервые описано Эвелин Фокс Келлер и Ли Сигел в статье в 1970 году. До того, как Келлер начала свои исследования, общепринятым считалось, что рои слизевиков образуются по команде клеток-лидеров, которые приказывают другим клеткам начать агрегацию.
| NetLogo |
| Solid Diffusion (model) | This model demonstrates a solid diffusion couple, such as copper and nickel. In a real laboratory, such experiment would take place at very high temperatures, for the process to take place in a reasonable amount of time (note that the diffusion coefficient varies exponentially with the inverse of the temperature). There are many mechanisms for diffusion in solids. In this model we demonstrate one of them, which is caused by missing atoms in the metal crystal. The locations, of the missing atoms are often called vacancies. Therefore, this type of diffusion mechanism is referred to as "vacancy diffusion". The extent to which the diffusion can happen depends on the temperature and the number of vacancies in the crystal. | NetLogo |
| Sugarscape model | Sugarscape model (сахарная модель) - один из методов(моделей) разработки искусственного общества. Модель стала популярна благодаря известной работе «Growing Artificial Societies». Является одной из простых моделей и прекрасным инструментом для обсуждения и экспериментального исследования ряда научных вопросов. Имеется некоторая окружающая среда — сахарный ландшафт, где в двумерном пространстве разбросан сахар — где-то больше, где-то меньше; и туда же помещены агенты-жуки, которые ползают по сахарному ландшафту по простым правилам: агенту надо есть сахар, и он перемещается туда, где сахара больше. Так они двигаются, поедают сахар, который появляется в той или иной точке тоже по каким-то законам. Наблюдая за поведением агентов на экране мы видим то, что Джошуа Эпштейн и Роберт Акстелл определили как прото-историю или Proto-Narrative
 | NetLogo |
| Team Assembly (model) | Эта модель коллаборативных сетей показывает, как поведение отдельных людей при формировании небольших команд для краткосрочных проектов может со временем привести к появлению множества крупномасштабных сетевых структур.
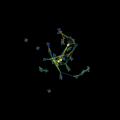 | NetLogo |
| The princess is collecting coins and planting flowers near her castle. | Принцесса около своего замка находит и собирает монетки, которые оставили туристы, чтобы вернуться, и на эти деньги украшает территорию, сажая разные цветочки.
 | StarLogo Nova |
| This is my fish! | Посмотрим, кто из нас действительно голоден! Пингвины пытаются забрать и съесть всю возможную рыбу. | StarLogo Nova |
| Traffic jams | Модель формирования и рассасывания дорожной пробки, реализованная в нескольких средах многоагентного моделирования | NetLogo StarLogo Nova Snap! |
| Urban Suite - Awareness | Модель определяет теоретический уровень «осведомленности» человека в городской среде на основе случайного контакта человека с информационными центрами. В модели информационными центрами являются любые источники обмена позитивной информацией. В этой модели каждый человек обладает некоторой степенью «осведомленности», которая измеряется в «очках осведомленности». Существует дискретный набор «уровней» осознания, которых могут достичь люди. Человек может быть «неосведомленным» (0–5 баллов), «осведомленным» (5–10 баллов), «хорошо информированным» (10–15 баллов) или «активистом» (более 15 баллов). Чтобы обрести осознанность, человек либо бежит в центр, где получает пять очков осознанности; или находится под влиянием хорошо информированного человека. Если одно из этих событий не произойдет в течение заданного временного шага (tick), человек потеряет одно очко осведомлённости (вплоть до нуля). Когда человек становится активистом (15 точек осознания), формируется новый центр. Новые информационные центры окрашены в синий цвет, а первоначальные информационные центры - в зеленый. Если никто не вступает в контакт с центром в течение заданного времени (см. ползунок НЕИСПОЛЬЗОВАНИЕ-ОГРАНИЧЕНИЕ), центр исчезает из мира. Если какой-либо информационный/рекламный метод или место не приносит результатов, в конечном итоге он будет закрыт. | NetLogo |
| Urban Suite - Economic Disparity | Когда в мире появляется новое место работы, оно случайным образом выбирает некоторое количество местоположений (управляемое ползунком КОЛИЧЕСТВО ИСПЫТАНИЙ) и выбирает то, которое имеет самую высокую цену (то есть стоимость земли). Поначалу это может показаться иррациональным, но в этой модели предполагается, что рабочие места перемещаются туда, где находится богатство. Если в определенной области денег больше, то есть более состоятельные люди, которые могут потратить эти деньги на товары и услуги. В этой модели есть два принципиально разных типа людей — «бедные» люди (показаны синим цветом) и «богатые» люди (показаны розовым цветом), и у них разные приоритеты. Оба типа людей желают располагаться недалеко от места работы. Однако богатые люди ищут место с хорошим качеством, не обращая внимания на цену, в то время как бедные люди ищут места с низкой ценой, не обращая внимания на качество. | NetLogo |
| Virus on a Network | Сетевая модель "Virus on a Network" может иметь несколько интерпретаций.
Первая из интерпретаций находится в плоскости информационной безопасности - распространение вируса по компьютерной сети. Вторая из возможных интерпретаций находится в плоскости социологии и управления - распространение инновационной идеи в организации (в частности, в образовательной организации, в школе). В этом случае модель можно использовать как инструмент для иллюстрации процесса распространения инноваций в зависимости от характеристик социального капитала. Каждый элемент модели находится в трех состояниях: вовлеченный (infected), восприимчивый (susceptible) или резистентный (resistant). Модифицированную модель Netlogo, а также результаты проведенных в BehaviorSpace экспериментов и скрипт в R для анализа результатов можно скачать по ссылке: https://github.com/mmyshkina/netlogo_innovation_idea_on_a_netwok | NetLogo R |
| Модель Лотки — Вольтерры | Моде́ль Ло́тки — Вольте́рры (модель Ло́тки — Вольтерра́) — модель взаимодействия двух видов типа «хищник — жертва», названная в честь своих авторов (Лотка, 1925; Вольтерра 1926), которые предложили модельные уравнения независимо друг от друга. | StarLogo Nova R Netlogo |
| Насосы и испарение | Модель физических процессов, в которой происходит испарение воды | StarLogo Nova |
| Охота морских коньков | Модель, которая показывает, каким образом увеличивается морской конек относительно того, сколько рыбы ему удастся съесть. | StarLogo Nova |
| Поезд и рыбы | На город, в котором царят только мирные взаимоотношения между женщинами и лягушками, нападают танки, замаскировавшись под поезд. Что происходит дальше? | StarLogo Nova |
| Собирание учеников в классы | 3 Учителя - черный, красный и желтый собирают учеников в свои классы | StarLogo Nova |
| Термиты | Модель термитника (муравейника), когда тупые, слабые и слабовидящие агенты перемещаются по полю и собирают на нём палочки. Есть версия "Термиты с журналом", когда все действия термитов над палочками записываются в лог-файл и потом можно построить графы команд, где в команду объединены термиты, носившие одни и те же палочки. | NetLogo StarLogo Nova |
| Термиты с журналом | Дополненная журналом, куда записываются все действия термитов над палочками, модель термитов. Представим себе, что у термитов есть журнал учета рабочих действий, куда они записывают все свои действия со щепочками. Т.е. если участник совершает какое-то результативное действие с chip, то он об этом действии оставляет запись в журнале. Для того чтобы проверить, что дают нам попутные записи в журнал, мы несколько видоизменили исходный текст модели Termites добавив к модели новые переменные и правила. В модели появилась переменная список WIKILOG, куда термиты записывают отчеты о своих действиях. В процедурах search-for-chip и put-down-chip были сделаны небольшие добавления. В модель была добавлена процедура, которая на основании записей в журнале устанавливает связь между агентами, которые перетаскивали одну и ту же палочку. | NetLogo |
| Футбольное поле с множеством мячиков | Модель сбора данных с поля, на котором множество игроков взаимодействуют со множеством мячиков. Модель используется для
| StarLogo Nova |
Страницы в категории «Model»
Показано 38 страниц из 38, находящихся в данной категории.