Sugarscape model

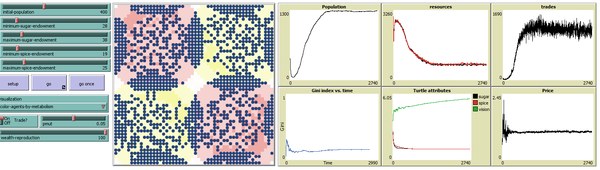
Описание модели	Sugarscape model (сахарная модель) - один из методов(моделей) разработки искусственного общества. Модель стала популярна благодаря известной работе «Growing Artificial Societies». Является одной из простых моделей и прекрасным инструментом для обсуждения и экспериментального исследования ряда научных вопросов. Имеется некоторая окружающая среда — сахарный ландшафт, где в двумерном пространстве разбросан сахар — где-то больше, где-то меньше; и туда же помещены агенты-жуки, которые ползают по сахарному ландшафту по простым правилам: агенту надо есть сахар, и он перемещается туда, где сахара больше. Так они двигаются, поедают сахар, который появляется в той или иной точке тоже по каким-то законам. Наблюдая за поведением агентов на экране мы видим то, что Джошуа Эпштейн и Роберт Акстелл определили как прото-историю или Proto-Narrative
Область знаний	NetSci, Биология, Экономика, Управление, Урбанистика
Веб-страница - ссылка на модель	https://ccl.northwestern.edu/netlogo/models/Sugarscape1ImmediateGrowback
Видео запись
Разработчики	Axtell, Epstein
Среды и средства, в которых реализована модель	NetLogo
Диаграмма модели
Описание полей данных, которые модель порождает
ODD protocol	DREAM О чём эта модель? Как устроена модель (правила внутри) Как пользоваться моделью На что следует обратить внимание Что стоит попробовать Расширение возможностей модели Функции среды программирования, которые использованы в этой модели Похожие модели

Основная модель в книге Growing Artificial Societies: Social Science From the Bottom Up (Complex Adaptive Systems)

Brewer, P., Ratan, A., 2019. Profitability, efficiency, and inequality in double auction markets with snipers. Journal of Economic Behavior & Organization 164, 486–499. https://doi.org/10.1016/j.jebo.2019.06.017

Использование модели на практике

Авторы «сахарной модели», Джошуа Эпштейн и Роберт Акстелл, проводили со своим творением всевозможные эксперименты, в частности сделали модель, где в качестве окружающей среды взяли карту США, и жуки ползали по всей Америке.

И в это же время компания Pizza Hut задалась вопросом, как создать широкую сеть своих заведений, где их разместить, чтобы получить как можно больше клиентов и соответственно доходов. Специалист, которому это было поручено, разработал свой проект, и тут ему в руки попал отчет о «сахарной модели». Сначала он решил, что идея была украдена у него, но затем встретился с Эпштейном и Акстеллом, они стали сотрудничать, и специалист из Pizza Hut даже смог улучшить свои результаты. Действительно, в качестве сахара можно взять людей — американцев. Они неравномерно разбросаны по стране — в Калифорнии больше, в Неваде меньше. А жуки, или агенты, — это ресторанчики Pizza Hut.

В дальнейшем модель стали усложнять, и она действительно практически превратилась в искусственное общество. Например, агенты могут делиться на мужчин и женщин, и тогда они ведут себя по разным правилам. Они могут не только съедать сахар, но и делать накопления — откладывать про запас, а потом, например, передавать по наследству — опять-таки по-разному: детям, или просто тому, кто им понравится, или всем поровну, и т. д. То есть можно задавать различные условия и наблюдать их последствия. Таким образом и появляются знания: вы берете какие-то правила, «вставляете» их в модель, запускаете и следите, к чему это приведет. Экономика появилась в «сахарной модели» простым способом: к сахару добавили сироп. Жуки стали есть сахар и сироп, и у одних оказалось больше сахара, у других сиропа, они начали встречаться и обмениваться — конечно, соблюдая определенные пропорции. Какое-то количество сахара можно обменять на некоторое количество сиропа — возникает цена. То есть на «сахарной модели» можно воочию увидеть, как появились цены — в тот момент, когда люди стали договариваться о пропорциях обмена одних вещей на другие.

Sugarscape Seasonal Migration

This third model in the NetLogo Sugarscape suite implements Epstein & Axtell's Sugarscape Wealth Distribution model, as described in chapter 2 of their book Growing Artificial Societies: Social Science From the Bottom Up (Complex Adaptive Systems). It provides a ground-up simulation of inequality in wealth. Only a minority of the population have above average wealth, while most agents have wealth near the same level as the initial endowment.

Неравенство полученного распределения можно описать графически - кривая Лоренца и количественно коэффициент Джини.