Small group discussion

Описание модели	Модель обсуждения в малой группе. Модель Различает роли студента и преподавателя — позволяет моделировать педагогические стратегии, а не только традиционные подходы к моделированию популяции агентов Агенты имеют убеждения о собственных состояниях и состояниях других агентов, которые изменяются в результате вербальных транзакций Учитывает конкуренцию и кооперацию как факторы, формирующие характер групповой дискуссии Предоставляет теоретическую перспективу для анализа индивидуального и группового развития вовлечённости в задачу (активность) и социальной вовлечённости с одноклассниками (дискурсивность) в независимых и модерируемых преподавателем малых группах
Область знаний	Социология, Лингвистика
Веб-страница - ссылка на модель
Видео запись
Разработчики
Среды и средства, в которых реализована модель	NetLogo
Диаграмма модели
Описание полей данных, которые модель порождает
Модель создана студентами?	Нет

Транзакция

Транзакция — это вербальное взаимодействие между двумя или более агентами, состоящее из

• Источник (Source Agent) — агент, который говорит
• Целевой агент (Target Agent) — агент или агенты, с которыми взаимодействует источник

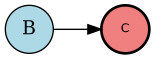
Диадная транзакция

Диадная транзакция (A B)

• Участвуют два агента (источник A и целевой агент B)
• Основной тип взаимодействия в парных обсуждениях

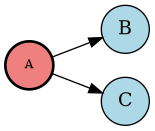
Триадная транзакция [A [B C]]

• Участвуют три агента: источник (A), первичная цель (B) и коллатеральная цель (C)
• Создаёт возможности для развития больших интерактивных групп
• Математически может быть представлена как: [math]\displaystyle{ \tau_{triadic} = S \to (P, C) }[/math], где S — источник, P — первичная цель, C — коллатеральная цель

Агенты

Каждый агент характеризуется двумя основными переменными:

1. Активность (Activity) [math]\displaystyle{ a_i(t) }[/math]
   • Отражает вероятность или склонность агента инициировать транзакцию
   • Интерпретируется как задачная вовлечённость
   • Начальное значение: случайная величина из равномерного распределения [math]\displaystyle{ a_i(0) \sim U(0.333, 0.667) }[/math]
   • Изменяется в результате участия в транзакциях
2. Дискурсивность (Discursivity) [math]\displaystyle{ d_{ij}(t) }[/math]
   • Вероятность или склонность агента i обращаться к конкретному агенту j
   • Интерпретируется как социальная вовлечённость с одноклассниками
   • Специфична для каждой пары агентов
   • Отражает сетевые свойства группы

Счастье агента

Счастье агента (Agent Happiness) - Счастье — взвешенное среднее активности и дискурсивности: [math]\displaystyle{ h_i(t) = \alpha \cdot a_i(t) + (1-\alpha) \cdot \bar{d}_i(t) }[/math]

Где

• [math]\displaystyle{ \bar{d}_i(t) }[/math] — средняя дискурсивность агента i ко всем другим
• [math]\displaystyle{ \alpha }[/math] — вес активности

Чувствительность к обучению (Overall Sensitivity)

Общая чувствительность (OS) — случайно назначаемый параметр, определяющий способность агента к обучению: [math]\displaystyle{ OS_i \sim U(0.05, 0.35) }[/math] Низкие значения OS ограничивают способность агента изменять своё состояние, тогда как высокие значения способствуют более быстрому обучению.

Базовые концепции статистики

1. Случайные переменные
   • Начальные значения активности: [math]\displaystyle{ a_i(0) \sim U(0.333, 0.667) }[/math]
   • Вероятность изменения состояния: стохастическое событие
2. Распределения вероятностей
   • Равномерное распределение для инициализации
   • Нормальное распределение для средних значений в группе
3. Корреляция и ковариация
   • Корреляция между [math]\displaystyle{ a_i(t) }[/math] и [math]\displaystyle{ \bar{d}_i(t) }[/math]
   • Ковариация между агентами в группе

Описательная статистика

1. Среднее значение активности в группе: [math]\displaystyle{ \bar{a}(t) = \frac{1}{n}\sum_{i=1}^n a_i(t) }[/math]
2. Дисперсия дискурсивности: [math]\displaystyle{ \sigma^2_d(t) = \frac{1}{n}\sum_{i=1}^n (d_i(t) - \bar{d}(t))^2 }[/math]

Модель генерирует данные для анализа:

1. Временной ряд активности каждого агента
2. Матрица смежности — дискурсивность между всеми парами агентов
3. Статистика транзакций — количество, типы и последовательность взаимодействий