Матрица смежности

Описание	Матрица смежности (англ. Adjacency matrix, Connectivity matrix) — математическая структура представления графа в виде матрицы, которая широко применяется в теории графов, сетевом анализе, а также при изучении групповых взаимодействий и командной деятельности.
Область знаний	Математика, Социология
Авторы
Поясняющее видео
Близкие понятия	Матрица, Граф
Среды и средства для освоения понятия	R, NetLogo

Матрица смежности (англ. Adjacency matrix, Connectivity matrix) — математическая структура представления графа в виде матрицы, которая широко применяется в теории графов, сетевом анализе, а также при изучении групповых взаимодействий и командной деятельности. Матрицы смежности как инструмент анализа графов начали использоваться в начале XX века в контексте теории графов. С развитием компьютерной техники и методов анализа социальных сетей (особенно в работах Милгрэма, Грановеттера и других социологов) они стали стандартным инструментом для представления и анализа сложных систем взаимодействий.

Определение и математическое описание

Матрица смежности графа [math]\displaystyle{ G }[/math] с конечным числом вершин [math]\displaystyle{ n }[/math] — это квадратная целочисленная матрица размера [math]\displaystyle{ n \times n }[/math], в которой значение элемента [math]\displaystyle{ a_{i,j} }[/math] равно числу рёбер из [math]\displaystyle{ i }[/math]-й вершины графа в [math]\displaystyle{ j }[/math]-ю вершину.

Математически матрица смежности [math]\displaystyle{ A(G) = (a_{ij}) }[/math] определяется следующим образом:

[math]\displaystyle{ a_{ij} = \begin{cases} 1, & \text{если вершины } v_i \text{ и } v_j \text{ смежны} \\ 0, & \text{в противном случае} \end{cases} }[/math]

Основные свойства

• Бинарность: Для простого графа (без петель и кратных рёбер) матрица смежности бинарна и содержит только значения 0 и 1
• Нулевая диагональ: Для графа без петель главная диагональ матрицы состоит из нулей ([math]\displaystyle{ a_{ii} = 0 }[/math])
• Симметричность: Для неориентированного графа матрица смежности всегда симметрична: [math]\displaystyle{ a_{ij} = a_{ji} }[/math]
• Степень вершины: Сумма элементов [math]\displaystyle{ i }[/math]-й строки равна степени вершины [math]\displaystyle{ v_i }[/math]: [math]\displaystyle{ \sum_{j=1}^{n} a_{ij} = \deg(v_i) }[/math]

Примеры матриц смежности

Граф	Матрица смежности	Описание
Граф из 3 связных вершин	[math]\displaystyle{ \begin{pmatrix} 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 0 \end{pmatrix} }[/math]	Полносвязный неориентированный граф [math]\displaystyle{ K_3 }[/math]
Граф с ориентированным ребром	[math]\displaystyle{ \begin{pmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \end{pmatrix} }[/math]	Ориентированный граф (циклический)
Граф из 4 изолированных вершин	[math]\displaystyle{ \begin{pmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{pmatrix} }[/math]	Пустой граф [math]\displaystyle{ O_4 }[/math]

Применение в анализе командной деятельности

Основная концепция

В контексте изучения командной деятельности и групповых дискуссий матрица смежности представляет собой мощный инструмент для визуализации и анализа социальных взаимодействий. Каждый член команды рассматривается как вершина графа, а взаимодействия между ними — как рёбра.

Основные применения:

• Выявление структуры команды: Матрица смежности позволяет определить, кто с кем взаимодействует в команде
• Анализ центральности узлов: Выявление ключевых участников, которые активнее всего взаимодействуют с коллегами
• Обнаружение подгрупп: Идентификация кластеров или сообществ внутри команды
• Анализ потоков информации: Понимание, как информация распространяется через команду

Метрики анализа социальных сетей

Метрика	Формула	Применение в команде
Центральность по степени (Degree Centrality)	[math]\displaystyle{ C_D(v_i) = \sum_{j=1}^{n} a_{ij} }[/math]	Выявляет наиболее активных членов команды, с которыми взаимодействуют многие коллеги
Центральность по посредничеству (Betweenness Centrality)	[math]\displaystyle{ C_B(v_i) = \sum_{s \neq i \neq t} \frac{\sigma_{st}(v_i)}{\sigma_{st}} }[/math]	Определяет «связующих звеньев» — людей, которые соединяют разные части команды
Центральность по близости (Closeness Centrality)	[math]\displaystyle{ C_C(v_i) = \frac{1}{\sum_{j=1}^{n} d(v_i, v_j)} }[/math]	Показывает, насколько быстро участник может донести информацию до остальных
Плотность графа (Graph Density)	[math]\displaystyle{ \rho = \frac{2e}{n(n-1)} }[/math]	Характеризует уровень связности команды (от 0 до 1)

Групповые дискуссии и анализ участия

При анализе групповых дискуссий матрица смежности фиксирует:

• Кто кому адресует высказывания (ориентированное ребро)
• Интенсивность взаимодействия между участниками (вес ребра)
• Паттерны коммуникации (кто инициирует диалоги, кто редко участвует)
• Равномерность распределения участия в дискуссии

Практическое применение: Анализ в R с использованием igraph

Пример: Анализ взаимодействий в команде проекта

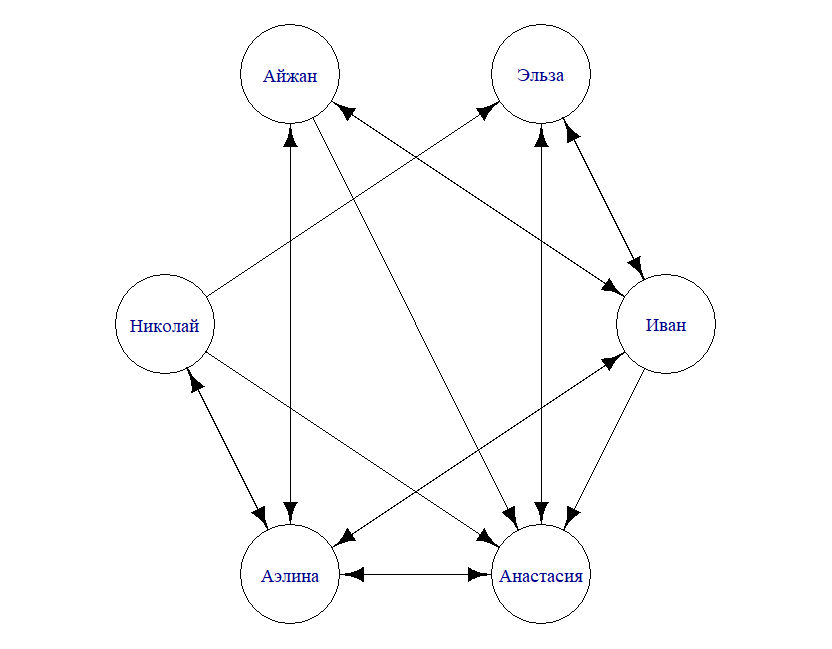
Рассмотрим команду из 6 человек, взаимодействующих во время групповой дискуссии. Ниже приведен пример кода на R для создания и визуализации сетевого графа на основе матрицы смежности.

# Загрузка библиотеки igraph
library(igraph)

# Определение матрицы смежности для команды
# Строки и столбцы: Иван, Эльза, Айжан, Николай, Аэлина, Анастасия
A <- matrix(c(
  0, 1, 1, 0, 1, 0,  # Иван взаимодействует с Эльзой, Айжан, Аэлиной
  1, 0, 1, 1, 0, 1,  # Эльза взаимодействует со многими
  1, 1, 0, 1, 1, 0,  # Айжан активна в коммуникации
  0, 1, 1, 0, 0, 1,  # Николай
  1, 0, 1, 0, 0, 1,  # Аэлина
  0, 1, 0, 1, 1, 0   # Анастасия
), nrow = 6, ncol = 6, byrow = TRUE)

# Создание графа из матрицы смежности
g <- graph_from_adjacency_matrix(A)

# Присвоение имен вершинам (членам команды)
V(g)$label = c("Иван", "Эльза", "Айжан", "Николай", "Аэлина", "Анастасия")

# Установка расположения вершин в виде круга
g$layout <- layout_in_circle

# Подготовка к визуализации: установка параметров окна
par(mar=c(0,0,0,0))

# Создание и вывод графика
plot(g, vertex.size=40, vertex.color="white", edge.color="black")

# Расчет метрик центральности
degree_centrality <- degree(g)
betweenness_centrality <- betweenness(g)
closeness_centrality <- closeness(g)

# Вывод результатов анализа
cat("Центральность по степени:\n")
print(degree_centrality)
cat("\nЦентральность по посредничеству:\n")
print(betweenness_centrality)
cat("\nЦентральность по близости:\n")
print(closeness_centrality)

# Вычисление плотности графа
density_value <- edge_density(g)
cat("\nПлотность графа (показатель связности):\n")
print(density_value)

Интерпретация результатов

Результаты анализа показывают:

• Высокая степень центральности указывает на активное участие в групповой дискуссии и взаимодействие со многими коллегами
• Высокая центральность по посредничеству у членов команды, которые связывают различные подгруппы
• Плотность графа показывает, насколько команда сплочена в своих взаимодействиях