Bootstrap
| Описание | Bootstrap - Бутстрэп (англ. bootstrapping) — это непараметрический метод статистического анализа, основанный на resampling данных с возвращением для оценки распределения статистики, доверительных интервалов и стандартных ошибок. Если у вас есть одна выборка, вы можете создать 1000 новых выборок из неё же (с возвращением), и использовать эти 1000 выборок вместо 1000 экспериментов. Бутстрэп полезен для малых выборок. Бутстрэп работает для любого распределения универсально. |
|---|---|
| Область знаний | Биология, Педагогика, Статистика |
| Авторы | Брэдли |
| Поясняющее видео | |
| Близкие понятия | Выборка |
| Среды и средства для освоения понятия | StatKey |
Бутстрэп в статистике (Bootstrap method)
Бутстрэп (англ. bootstrapping) — это непараметрический метод статистической инференции, основанный на resampling данных с возвращением для оценки распределения статистики, доверительных интервалов и стандартных ошибок.
[math]\displaystyle{ \theta^* = \frac{1}{B} \sum_{b=1}^B t(\mathbf{X}^{*b}) }[/math] ([math]\displaystyle{ \theta^* = \frac{1}{B} \sum_{b=1}^B t(\mathbf{X}^{*b}) }[/math]).
| Ситуация | n | Распределение | Рекомендация | Почему |
|---|---|---|---|---|
| Реальные данные (опрос) | 50–100 | Неизвестно | Bootstrap | Мало данных, неизвестное распределение, универсален |
| Реальные данные | > 1000 | Неизвестно | t-test или Bootstrap | ЦПТ работает, оба метода дают похожие результаты |
| Реальные данные | 50–100 | Нормально (проверили) | t-test | Формула применима, результаты точны |
| Симуляция NetLogo | n > 100 | Из модели | Обычная статистика (CI из SE) | Есть естественная репликация, бутстрэп не нужен |
| Симуляция NetLogo | n > 1000 | Из модели | Обычная статистика | Ещё больше данных, совсем не нужен бутстрэп |
| Симуляция NetLogo | n = 50 | Из модели | Bootstrap? | Маловероятно, но теоретически можен |
Принцип работы метода
Бутстрэп предполагает многократное (обычно 1000–10000 раз) извлечение выборок с возвращением из исходного датасета размером \( n \), вычисление целевой статистики для каждой и построение эмпирического распределения.[math]\displaystyle{ \mathbf{X}^* = \{X_1^*, \dots, X_n^*\} \sim \text{empirical distribution of } \mathbf{X} }[/math] ([math]\displaystyle{ \mathbf{X}^* = \{X_1^*, \dots, X_n^*\} \sim \text{empirical distribution of } \mathbf{X} }[/math]). Это позволяет оценивать квантили для доверительных интервалов без аналитических формул.
Например, в моделировании рынка труда учителей средняя удовлетворенность может варьироваться стохастически; бутстрэп дает распределение этой статистики для проверки гипотез о стабильности системы.
Bootstrap работает, потому что ЦПТ гарантирует, что даже если ваши данные "грязные" и не нормальные, средние из повторных выборок будут нормальными. Это позволяет вычислять доверительные интервалы без знания истинной популяции.
| Description | |
|---|---|
| Центральная предельная теорема | Центра́льные преде́льные теоре́мы (ЦПТ) — класс теорем в теории вероятностей, утверждающих, что сумма достаточно большого количества слабо зависимых случайных величин, имеющих примерно одинаковые масштабы (ни одно из слагаемых не доминирует, не вносит в сумму определяющего вклада), имеет распределение, близкое к нормальному. Так как многие случайные величины в приложениях формируются под влиянием нескольких слабо зависимых случайных факторов, их распределение считают нормальным. При этом должно соблюдаться условие, что ни один из факторов не является доминирующим. Центральные предельные теоремы в этих случаях обосновывают применение нормального распределения. |
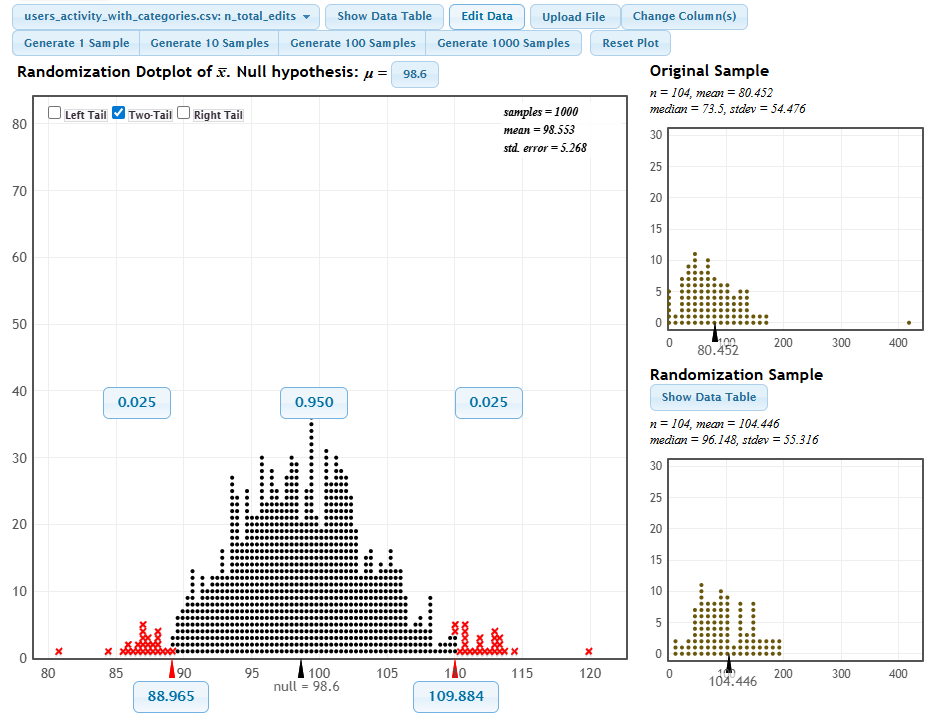
Реальный пример с активностью студентов
Использование в проектах NetLogo
Нет никакого смысла! В проектах по "выращиванию данных" (data farming) в NetLogo, таких как модель Teacher Satisfaction (model), Модель симулирует удовлетворенность учителей (mean_satisfaction-all), текучесть кадров и вакансии школ в зависимости от радиуса мобильности, зарплаты и качества школ.
| Контекст | Данные | Размер | Bootstrap? | Почему | Пример |
|---|---|---|---|---|---|
| Реальное исследование | Опрос студентов | n=50–100 | ДА! | Универсален, не требует предположений | Филологи vs Историки |
| Реальное исследование | Опрос студентов | n>1000 | Опционально | ЦПТ гарантирует нормальность | Массовый опрос |
| Многоагентное моделирование | BehaviorSpace | n=1 запуск | Не рекомендуется | Нужна репликация, не бутстрэп! | Teacher Satisfaction (1 раз) |
| Многоагентное моделирование | BehaviorSpace | n=1000 запусков | НЕТ | Уже есть распределение | Teacher Satisfaction (1000 раз) |
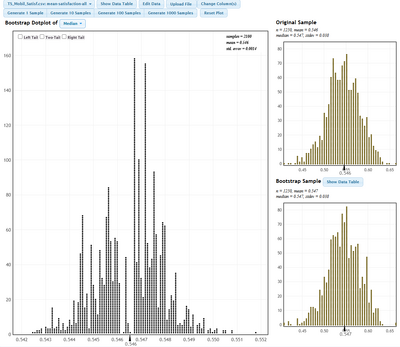
StatKey как инструмент анализа
StatKey — онлайн-апплет для визуализации бутстрэпа и рандомизации, идеален для данных из ABM как поле для быстрого прототипирования интервалов без программирования. Загрузите колонку mean_satisfaction-all в StatKey (Theoretical Distribution → One Quantitative → Bootstrap CI for Mean), сгенерируйте 5000 сэмплов для перцентильного интервала.
В контексте Teacher Satisfaction: копируйте данные в StatKey для оценки вариабельности mean_school_vacancy_rate, визуализируя распределение бутстрэп-средних
Пример вывода: для сэмпла std=0.020, бутстрэп дает CI шириной ~0.01, подтверждая стабильность модели при unemployment_rate ~0.003.
CODAP предоставляет плагин Bootstrap для resampling данных и моделирования доверительных интервалов без программирования