Нелинейная регрессия

Описание	Нелинейная регрессия – это статистический метод, который помогает нам понять и описать сложные зависимости между разными величинами, когда эти зависимости нельзя описать простой прямой линией. Нелинейная регрессия — это вид регрессионного анализа, в котором экспериментальные данные моделируются функцией, являющейся нелинейной комбинацией параметров модели и зависящей от одной или более независимых переменных. Такая модель описывает зависимость результативной переменной от одной или нескольких объясняющих переменных с помощью нелинейной функции, и параметры в уравнении регрессии входят не в линейной форме.
Область знаний	Экономика, Статистика
Авторы
Поясняющее видео
Близкие понятия	Регрессия
Среды и средства для освоения понятия	Economic Disparity, R, CODAP

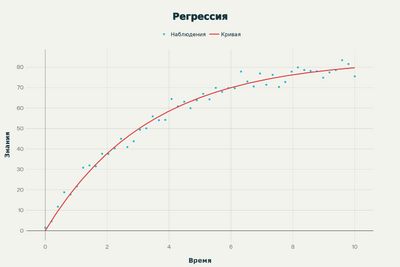
Представьте себе, как студенты изучают новый предмет. В первые дни они быстро схватывают основы, потом темп обучения замедляется, и в конце концов достигается некий предел знаний. Такую зависимость нельзя описать прямой линией – это классический пример нелинейной зависимости, которую можно смоделировать с помощью нелинейной регрессии.

В общем виде это выглядит так: [math]\displaystyle{ y = f(x, \beta) + \varepsilon }[/math]

где

• [math]\displaystyle{ y }[/math] — зависимая переменная,
• [math]\displaystyle{ x }[/math] — независимая переменная (или переменные),
• [math]\displaystyle{ \beta }[/math] — параметры модели,
• [math]\displaystyle{ f(x, \beta) }[/math] — нелинейная функция связи,
• [math]\displaystyle{ \varepsilon }[/math] — ошибка.

Это определение различает нелинейные регрессии по самим переменным (например, полиномиальная зависимость) и по параметрам (например, экспоненциальная или степенная функции), и отмечает, что такие зависимости нельзя свести к линейным комбинациям параметров стандартными преобразованиями. Аппроксимация выполняется итерационными методами.

Существует два основных типа нелинейных регрессий:

1. Нелинейные по переменным, линейные по параметрам

• Пример: [math]\displaystyle{ y = \beta_0 + \beta_1 x + \beta_2 x^2 }[/math] (полиномиальная регрессия)
• Такие модели можно преобразовать в линейные

2. Нелинейные по параметрам

• Пример: [math]\displaystyle{ y = \beta_1 e^{\beta_2 x} }[/math] (экспоненциальная модель)
• Требуют специальных методов решения