Сетевые образовательные сообщества: анализ больших данных
| Описание события | Большие данные в образовании: от профильного образования до квалификации - // Патаракин Е.Д., д.пед.наук, доцент, Московский Городской Педагогический Университет, Высшая Школа Экономики |
|---|---|
| Тип события | Мастер класс |
| Начало | 2023-11-30T12:30:00.000Z |
| Окончание | 2023-11-30T14:00:36.000Z |
| color | green |
| Адрес события | https://bigdata-edu.com/conference-2023.php |
| Видео запись события | https://www.youtube.com/watch?v=Dgz8nNeVB50 |
| Среды и средства, которые использовались в рамках события | SNA, NetLogo |
| Формируемые в рамках события компетенции | |
| Область знаний | NetSci, Педагогика, Большие данные |
| Местоположение | 56° 17' 36.63" N, 44° 2' 27.06" E |
| Формат реализации | |
| Карта |
Аннотация
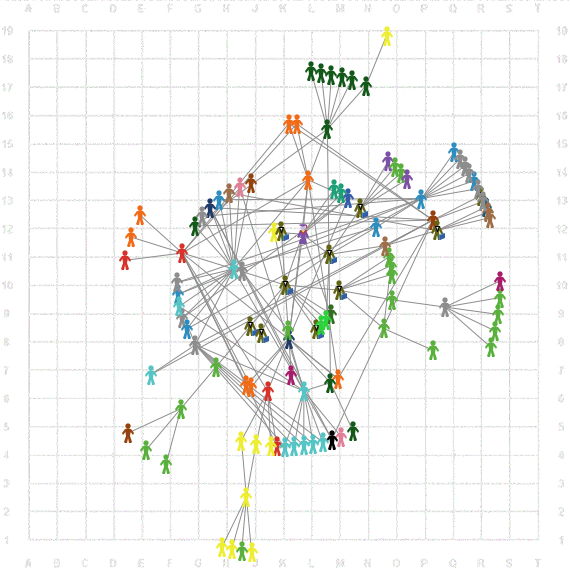
Мастер-класс основан на событиях, которые происходили с участниками совместной сетевой деятельности в сетевых сообществах. Мы исследовали цифровые следы, которые оставляли участники совместной деятельности в электронных библиотеках при создании совместные статей и разметке этих статей общими ключевыми словами; в различных категориях вики проектов при создании и редактировании совместных статей; в студиях и коллекциях различных сообществах обучения программированию при создании и видоизменении кода проектов; внутри школьных доменов при совместном создании, редактировании и использовании документов, презентаций, таблиц и диаграмм; в цифровых образовательных репозиториях при создании, запуске, копировании и видоизменении сценариев уроков. Во всех случаях мы использовали общую схему сетевого анализа, когда связи между агентами деятельности возникают в результате совместного создания или редактирования цифровых объектов.
- Ключевые слова
- сетевой анализ, сетевые сообщества, большие данные
Введение
Сетевой анализ, используемый в социальных науках, является модификацией исследовательского инструментария, который применяется в самых разных областях: в биологии, экономике, логистике, физике и т. д. Эта модификация носит официальное название «Social Network Analysis» («анализ социальных сетей»), однако во многих работах социальных аналитиков его обозначают просто как «сетевой анализ». Это направление современной вычислительной (или, как часто используя кальку с английского языка говорят «компьютерной») социологии, посвященное описанию и анализу связей, возникающих в ходе социального взаимодействия (в первую очередь – коммуникации) и приводящих к образованию единой структуры – социальной сети.
При использовании методов SNA ключевым является описание характеристик, выражающих плотность, интенсивность и пространственную координацию социальных связей. Благодаря этому становится возможным выделять в рамках исследования структурные единицы в системе социальных отношений («узлы», «блоки», «клики», «кусты»). Причем в качестве результатов проведенного анализа могут быть предъявлены не только явно обозначенные участниками рассматриваемой социальной группы взаимодействия и отношения, и выявленные в результате сетевого анализа скрытые связи. Это позволяет брать в качестве объекта анализа не только явно выявленную сеть прямых отношений участников, но и сеть опосредованных социальных взаимодействий, в рамках которой акторы (от аctor – деятель), также называемые «агентами», взаимодействуют с некоторыми общими объектами, и сеть связей возникает благодаря учету этих взаимодействий.
Предметом сетевого анализа является структура связей и отношений между людьми и объектами, входящими в разнообразные и разномасштабные общности. Традиционно для обозначения отдельного элемента социальной сети используют понятие «узел», если речь идет об исследованиях прикладного математического характера, или «актор», если подразумевается социологические исследования.
Построение карт сетевых отношений между акторами различной природы основывается на сетевых характеристиках узлов и рёбер. С точки зрения формального математического описания социальная сеть, образованная n акторами представляет собой граф [math]\displaystyle{ G=(V,E) }[/math] в котором множество [math]\displaystyle{ V={1,2,…,n} }[/math] представляет конечное множество вершин (агентов), а множество E содержит ребра, отображающие их взаимодействие. Сетевая плотность - общая характеристика сетевой структуры равная соотношению имеющихся и максимально возможных связей в социальной группе. Показатель кластеризации характеризует степень взаимодействия между собой ближайших соседей рассматриваемого актора и представляет собой локальную характеристику сети. В большинстве сетей, если актор А соединен с актором В, а актор В с актором С, то существует большая вероятность, что акторы А и С соединены – друзья наших друзей, обычно, также являются и нашими друзьями. Параметр центральности актора является одним из наиболее часто востребованных при использовании методов SNA. Содержательный смысл расчета показателя центральности состоит в определении того, насколько неравномерно распределена власть-влияние в смысле, определяемом выбранными видами связей в социальной группе, представленной графом. Таким образом, C_D=0 тогда и только тогда, когда отсутствует преимущество в центральности любого актора, а C_D=1 единственно возможно, тогда, когда доминирует единственная вершина. Показатель централизации также называют «центральность группы».
В последние годы активно развивается Science of Team Science - наука о командных научных исследованиях. Эта область представляет одно из направлений гуманитарных вычислительных наук, цифровой и сетевой социологии. «Командная наука» исследует поведение людей в современных командах сложных технологических средах, которые во многом определяют то, как протекает совместная работа и совместное обучение. При этом для анализа положения конкретного агента, как правило, используются сетевые характеристики, перечисленные выше. Степень центральности показывает, кто является наиболее активным узлом в сети. Измеряется количеством связей с другими узлами в сети. Центральность (в любой из интерпретаций) показывает, насколько данный узел близок по отношению к другим узлам в сети. В соответствие с теорией сетей большое количество взаимодействий узла может не только изменить позицию узла в сети, но также и изменить позиции других узлов.
Сообщества авторов совместных статей в электронных библиотеках
«Командная наука» исследует поведение людей в современных командах сложных технологических средах, которые во многом определяют то, как протекает совместная работа и совместное обучение. научный подход предполагает, что несколько человек работают на достижение общей научной цели. При этом размер команд может варьировать от пар участников (диад), до крупных команд, в состав которых входят более мелкие команды.
Развитие командной науки (Team Science) стало возможным благодаря накоплению огромных массивов библиографических данных и разработке инструментов, которые сделали работу с такими данными доступными для широкого круга исследователей. В отношении неявных научных групп разработаны методы исследования, как правило, включающие библиографический и сетевой анализ, которые приводят к выделению графов, объединяющих ученых, принадлежащих к одной группе. Мы использовали методы библиографического анализа баз данных научного цитирования Web of Science, Scopus и ACM Digital Library В качестве средства библиографического анализа был выбран VOS viewer - средство, которое динамично развивается с 2009 года и используется для выявления и визуального представления сетевых отношений как между авторами, так и между ключевыми словами публикаций.
В первом примере качестве основного источника данных для библиометрического анализа взаимоотношений авторов, связанных с тематикой вычислительного мышления мы использовали материалы цифровой библиотеки ассоциация вычислительной техники (ACM Digital Library) – dl.acm.org
| Description | |
|---|---|
| ACM Digital Library | Цифровая библиотека ассоциации вычислительной техники — архив журналов, газет и материалов конференций организации. Онлайн-сервисы включают форумы, такие как Ubiquity и Tech News digest. |
Выбор этого источника связан с тем, что цифровая библиотека в течение почти семидесяти лет целенаправленно собирает работы, связанные с использованием компьютеров в различных сферах человеческой деятельности и здесь ожидаемо можно проследить историю обсуждения понятия «вычислительное мышление», различные подходы к вычислительному мышлению. Поисковый запрос к цифровой библиотеке ACM «computational thinking» с ограничением временного периода 2002 – 2022 выглядит следующим образом:
- [All: “computational thinking”] AND [Publication Date: (2002 To 2022)]
Запрос позволил получить 1680 записей в формате BIB о публикациях по теме вычислительного мышления. Обработка – слияние данных, проверка записей и удаление дубликатов осуществлялось в библиографическом менеджере Zotero [5,6], поскольку он поддерживает различные формы работы с исходными текстами публикаций, обеспечивает экспорт из различных библиотек и импорт в различные системы анализа и представления библиографических данных. После удаления дубликатов число записей составило 1645. Для выявления и визуального представления сетевых отношений как между авторами, так и между ключевыми словами публикаций мы использовался пакет VOS viewer, предварительно экспортировав данные в формат RIS.
Сеть понятий
Сеть авторов
В сети авторов, исследующих вычислительное мышление и такие понятия как решение проблем, абстракция и алгоритмизация, блочное программирование, программирование без компьютера, оценивание, учебная аналитика и масштабируемый дизайн игр соответствуют три группировки авторов, расположенные в верхней части рисунка.
Первая группировка, окрашенная в свело-зелёный цвета, ключевой фигурой которой на схеме является Александр Репеннинг (блочные языки программирования, масштабируемый игровой дизайн, теория зоны ближайшего потока). Рядом с первой группой расположена вторая группа, так же окрашенная в светло-зелёный цвет. Ключевым игроком в этой группе на схеме является Ясмин Кафаи. Исходно авторы этой группы связаны с MIT Media Lab, разработкой различных версий программной среды Logo, наиболее успешным примером которой является среда Scratch. Через связующего игрока Карен Бренна эта группа связана c оранжевый кластером, в центре которого находится Диана Франклин. Необходимо отметить, что связующим игроком, объединяющим оранжевый кластер с другими расположенными ниже группировками, является создатель языка NetLogo Ури Виленский.
Формат статьи не позволяет читателям самостоятельно исследовать группировки авторов, но это можно сделать при помощи интерактивного апплета, который доступен по адресу:
Сообщества авторов совместных вики-страниц
Внутри вики и вики-подобных систем коллективного редактирования гипертекстов, каждый автор может создавать и редактировать любую страницу. Действия над страницей разнообразны: проверить содержание, поправить форматирование, добавить иллюстрации, классифицировать страницу при помощи категорий. Вся история изменений страницы записывается в историю версий. Современные вики площадки, использующие в качестве своего движка MediaWiki открывают исследователям доступ к своим данным через MediaWiki API. Процесс формирования запросов облегчается присутствием на площадках специальных API песочниц, где исследователи могут тренироваться делать свои запросы к системе MediaWiki. Как правило, результаты запроса возвращаются в виде JSON файла, который можно представить в виде схемы при помощи языка PlantUML
| Description | |
|---|---|
| PlantUML | PlantUML позволяет генерировать диаграммы (по большей части в нотации UML) в виде текста, описывающего элементы и связи между ними. |
- Digida - Служебная:ApiSandbox
- WikiPedia https://ru.wikipedia.org/wiki/Служебная:ApiSandbox
Для некоторых вики площадок возможность визуального анализа взаимоотношений участников, совместно редактирующих статьи, была предусмотрена в рамках дизайна самой площадки. Например, для проекта letopisi.org мы разработали специальное расширение – extension, которое позволяет увидеть связи между статьями и авторами для любой страницы и категории страниц. Для этого достаточно на странице или категории нажать на вкладку wikigramma и получить и диаграмму и код этой диаграммы на языке dot пакета Graphviz.
| Description | |
|---|---|
| Graphviz | Graphviz — это разработанный специалистами лаборатории AT&T пакет утилит по автоматической визуализации графов, заданных в виде текстового описания. Пакет распространяется с открытыми исходными файлами и работает на всех операционных системах, включая Windows, Linux/Unix, Mac OS. Самой интересной программой пакета является «dot», автоматический визуализатор направленных графов, который принимает на вход текстовый файл со структурой графа, а на выходе формирует граф в виде графического, векторного или текстового файла. |
Код диаграммы можно редактировать и анализировать в сетевых сервисах, как это показано на рисунке

Сообщества авторов кода программ
Среди сообществ, авторы которых обмениваются кодом программ, наиболее известен GitHub с его с возможностью хранить репозиторий проекта и все его изменения.
| Description | |
|---|---|
| GitHub | Социальная сеть программистов, с возможностью хранить репозиторий проекта и все его изменения. GitHub - контроль доступа, багтрекинг, управлением задачами и вики для каждого проекта. Используется прежде всего для поддержания версий кода |
Для открытых проектов, а все бесплатные проекты на GitHub открыты по умолчанию, для любого участника существует возможность создания новой собственной версии репозитория. В этом случае этот участник становится новым хозяином и может развивать проект как собственный. На основании общих, но видоизмененных принципах GitHub, построены и разнообразные репозитории обучающего кода в таких системах совместной деятельности как Scratch, Snap!, StarLogo Nova, NetLogo, и целый ряд других.
Основные действия участников: размещение (публикация) кода, создание версий, оценивание, комментирование. Так же как и для MediaWiki для Scratch поддерживается API, что позволяет исследователям получать по запросу информацию, в виде JSON файла, который можно представить в виде схемы при помощи языка PlantUML. Например, на рисунке представлен результат запроса * https://api.scratch.mit.edu/studios/4902931
Мы провели сетевой анализ взаимоотношений участников нескольких скретч-студий на основе их действий по публикации и комментированию проектов. Кроме того, что мы можем работать с данными студии о проектах, мы можем работать с данными отдельных участников и устанавливать между ними связи на основании того, кто из них кого отслеживает.
Сообщества авторов документов внутри школьных доменов
В качестве источника данных о действиях учителей в школьной сети можно использовать записи о действиях с документами в доменах Google Apps для образования. В данном примере мы получили их в виде таблицы приблизительно в 90 000 записей. Каждая запись при этом представляет собой информацию о действии, совершенном пользователем (участником, зарегистрированном в домене), по отношению к объекту, хранящемуся в домене, имеющему конкретный идентификационный номер и конкретного автора. При анализе использовались 2 типа действий субъекта: создание и редактирование. На рисунке представлена позиция, которая сложилась на компьютерной карте совместной деятельности внутри школьной информационной системы после 4-х тысяч действий, совершенных участниками.
Сообщества авторов сценариев уроков в сетевых репозиториях
В последнем пример представляем совместную деятельность участников московской электронной школы созданию и повторному использованию сценариев уроков. Принципы анализа совместной деятельности внутри этого образовательного репозитория описаны в статье «Незримый колледж МЭШ». Для обработки данных, их визуализации и проведения статистического анализа мы использовали возможности языка R.
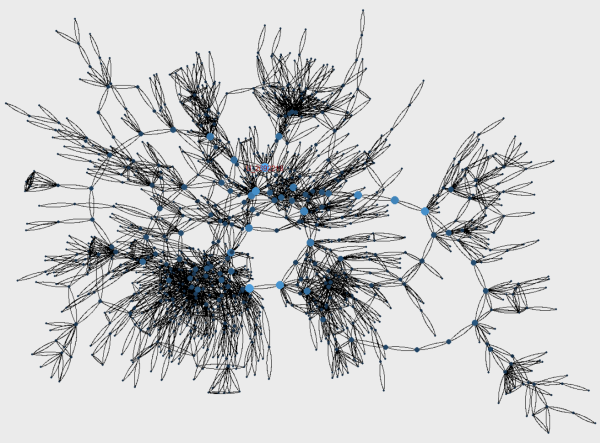
В данной статье представлена процедура выделения участников из фракции реципрокного копирования сценариев уроков. Исходно датасет содержал данные о действиях 64 тысяч учителей, которые сотрудничают внутри репозитория цифровых объектов Московской электронной школы. Последовательная фильтрация заключалась в том, что мы выделили тех, кто создавал собственные сценарии, а среди них отобрали тех, кто связан взаимными связями через взаимное копирование учебных сценариев. В результате мы получили граф из 145 отдельных компонентов и из этого графа отобрали только главный компонент.
Главный компонент содержит 1174 узла и 17928 связей, а на остальные 144 компоненты приходится всего 378 узлов и 3421 связь. Для того, чтобы объяснить объединение 75 % учителей, копирующих друг у друга сценарии уроков, в составе гигантской компоненты, мы использовали модель формирования команд Team Assembly (model) внеся в неё изменения, отражающие специфику репозитория московской электронной школы.
Во-первых, мы снизили минимальное число участников, необходимое для образования команды с трех до двух, поскольку в МЭШ часто наблюдаются группы-диады. Во-вторых, мы увеличили время пребывания агента в активном состоянии до того, как он покинет рабочую среду в силу своего возраста. После этих изменений мы поставили эксперимент со следующими условиями, записанными в BehaviorSpace:
["max-downtime" 800]
["team-size" 2]
["p" [10 5 75]]
["q" 52]
В качестве независимой переменной использовалось значение p – вероятность выбора новичков в качестве партнера по команде опытного участника, уже входящего в состав группы. В качестве измеряемой величины в 10 прогонах каждой серии эксперимента фиксировался процент участников, входящих в состав гигантской компоненты, после 800 циклов модели. Результаты в виде графика boxplot представлены на рисунке, и можно сделать предварительные выводы, что заметное изменение воздействия величины p на величину гигантской компоненты происходит в интервале 35 – 45 %, и выявленное для МЭШ объединение 75 % учителей может быть объяснено тем, что вероятность выбора опытного участника, уже входящего в состав группы, составляет не менее 60 %