Flocking (model)
| Описание модели | Модель самопроизвольного формирования стаи в результате действий множества участников (птиц, рыб, людей). Модель формирования стаи - это классическая агентно-ориентированная модель, основанная на оригинальных моделях Рейнольдса (1987). Модель демонстрирует, что стаи птиц могут возникать даже в отсутствии специальных птиц-вожаков, которые ведут всех за собой. Скорее, каждая птица следует общему же набору правил, и из выполнения всеми простых правил появляются стаи. Каждая птица следует трем правилам: «выравнивание», «разделение» и «сплоченность».
Правило «разделения» имеет приоритет над двумя другими, что означает, что если две птицы приближаются друг к другу, они всегда будут разделяться. В этом случае два других правила отменяются до тех пор, пока не будет достигнуто минимальное разделение. Эти три правила влияют только на направление птицы. Каждая птица всегда движется вперед с одинаковой постоянной скоростью. Правила удивительно надежны и могут быть адаптированы к скоплению насекомых, стаям рыб и паттернам «V» стаи гусей (Stonedahl & Wilensky, 2010a). |
|---|---|
| Область знаний | NetSci, Биология, Информатика, Управление |
| Веб-страница - ссылка на модель | https://ccl.northwestern.edu/netlogo/models/Flocking |
| Видео запись | |
| Разработчики | |
| Среды и средства, в которых реализована модель | Snap!, StarLogo Nova, NetLogo, Scratch |
| Диаграмма модели | |
| Описание полей данных, которые модель порождает | |
| Модель создана студентами? | {{{Student-created}}}«{{{Student-created}}}» — не булево значение (да/нет). |
ODD protocol
см. понятие Flocking
О чём эта модель?
Эта модель - попытка имитировать стаю птиц. (Результирующее движение также напоминает косяки рыб.) Стаи, которые появляются в этой модели, никоим образом не создаются и не ведутся специальными птицами-лидерами. Скорее, каждая птица следует точно такому же набору правил, из которых появляются стаи.
Как устроена модель (правила внутри)
Птицы следуют трем правилам: «выравнивание», «разделение» и «сплоченность».
- «Выравнивание» означает, что птица поворачивается так, чтобы двигаться в том же направлении, что и ближайшие птицы.
- «Сплоченность» означает, что птица будет двигаться к другим ближайшим птицам.
- «Разделение» означает, что птица поворачивается, чтобы избежать столкновения с другой птицей, которая летит слишком близко.
Когда две птицы находятся слишком близко, правило «разделения» отменяет действие двух других, которые деактивируются до тех пор, пока не будет достигнуто минимальное разделение.
Эти три правила влияют только на направление птицы. Каждая птица всегда движется вперед с одинаковой постоянной скоростью.
Как пользоваться моделью
Сначала определите количество птиц, которое вы хотите использовать в симуляции, и установите ползунок POPULATION на это значение. Нажмите SETUP, чтобы создать птиц, и нажмите GO, чтобы они начали летать.
Настройки по умолчанию для ползунков обеспечат достаточно хорошее поведение стаеобразования. Однако вы можете поиграть с ними, чтобы получить вариации поведения
Ползунок TURN-ANGLE регулирует максимальный угол, на который птица может повернуть в соответствии с каждым правилом.
- VISION - это расстояние, на котором каждая птица может видеть вокруг себя на 360 градусов.
На что следует обратить внимание
- Центральное место в модели занимает наблюдение, что стаи формируются без лидера.
- В этой модели не используются случайные числа, за исключением исходного положения птиц. Плавное, реалистичное поведение птиц полностью определяется детерминированными правилами.
- Также обратите внимание, что каждая стая динамична. Не гарантируется, что стая, однажды собравшееся, удержит всех своих членов. Как вы думаете, почему это так?
- Через некоторое время после запуска модели все птицы будут иметь примерно одинаковый курс. Почему?
- Иногда птица отрывается от своей стаи. Как это произошло? Вам может потребоваться замедлить модель или запустить ее шаг за шагом, чтобы наблюдать это явление.
Что стоит попробовать
- Поиграйте с ползунками, чтобы увидеть, сможете ли вы получить более плотные стаи, более рыхлые стаи, меньшее количество стай, большее количество стай, большее или меньшее разделение и объединение стай, более или менее перестановку птиц внутри стай и т. Д.
- Вы можете полностью отключить правило, установив ползунок этого правила на ноль. Достаточно ли одного правила, чтобы произвести хоть какое-то стайство? А как насчет двух правил? Чего не хватает в результирующем поведении, когда вы опускаете каждое правило?
- Будет ли работа модели в течение длительного времени производить статичную стаю? Или птицы никогда не сойдутся в неизменном строю? Помните, что в этой модели не используются случайные числа.
Расширение возможностей модели
- В настоящее время птицы могут «видеть» все вокруг себя. Что произойдет, если птицы могут видеть только перед собой? Для этого можно использовать примитив in-cone.
- Есть ли способ получить V-образные стаи, как перелетные гуси?
- Что произойдет, если вы поставите стены по краям мира, через которые птицы не могут перелететь и от которых они будут ?
- Сможете ли вы заставить птиц облетать препятствия посреди мира?
- Что бы произошло, если бы вы дали птицам разные скорости? Например, вы можете заставить птиц, которых нет рядом с другими птицами, летать быстрее, чтобы догнать стаю. Или вы можете имитировать уменьшение сопротивления воздуха, которое птицы испытывают при совместном полете, заставляя их летать быстрее, когда они находятся в группе.
Есть другие интересные способы сделать птиц отличными друг от друга? Популяции могут быть случайными, или у вас могут быть разные «виды» птиц.
Функции среды программирования, которые использованы в этой модели
Обратите внимание на необходимость специальной процедуры subtract-headings для усреднения направления групп. Простое вычитание чисел или их усреднение не дает ожидаемых результатов из-за разрыва, когда heading возвращаются к 0, когда они достигают 360.
- turn-at-most (subtract-headings new-heading heading) max-turn
- subtract-headings heading1 heading2
- Computes the difference between the given headings, that is, the number of degrees in the smallest angle by which heading2 could be rotated to produce heading1. A positive answer means a clockwise rotation, a negative answer counterclockwise. The result is always in the range -180 to 180, but is never exactly -180.
Похожие модели
- Мотыльки
- Форимирование V-образных стай
Примеры
- https://eater.net/boids - пример модели
Модель в Scratch
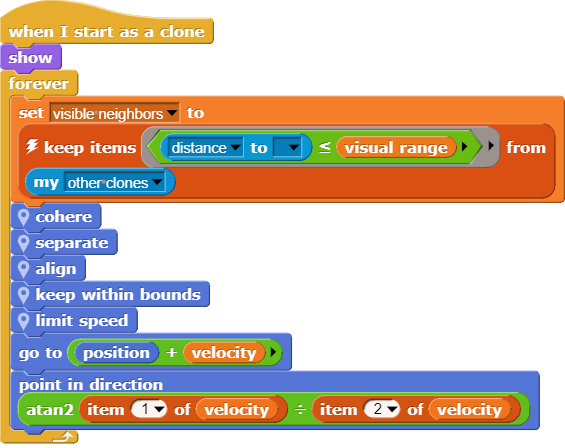
Модель в Snap!
- Пример того, как можно Обратиться_к_объектам_по_их_свойствам
Модель в StarLogo Nova
NetLogo