Эксперименты с моделью Urban Suite - Economic Disparity
ОПИСАНИЕ МОДЕЛИ
| Description | |
|---|---|
| Economic Disparity | Модель «Экономическое неравенство» представляет собой симуляцию городской среды, в которой две категории населения — богатые и бедные — выбирают место жительства, учитывая три ключевых параметра: стоимость земли, качество территории и близость к рабочим местам. Модель иллюстрирует процессы пространственной сегрегации по доходам, формирование кластеров услуг в более состоятельных районах и динамическое изменения характеристик территории под влиянием социально-экономического состава населения. Она служит инструментом для изучения взаимосвязи социально-экономических факторов и распределения населения, а также демонстрирует принципы гедонистического выбора и положительную обратную связь в городской экономике. Каждый агент действует согласно собственным правилам и целям, что делает модель более реалистичной по сравнению с подходами, основанными на оптимизации общесистемных критериев. Изучение эмерджентных свойств. Модель показывает, как индивидуальные предпочтения агентов приводят к крупномасштабным структурам - сегрегации населения по доходам и кластеризации услуг в более состоятельных районах. Это демонстрирует концепцию эмерджентности в сложных системах. |
Модель Urban Suite - Economic Disparity представляет упрощённую городскую экономическую систему, где агенты с различным социально-экономическим статусом конкурируют за землю в городском пространстве. Модель исследует процессы пространственной сегрегации и формирования экономического неравенства в городской среде. В модели есть фиксированные рабочие места (серые квадраты), распределённые по городской территории. Агенты стремятся минимизировать расстояние до ближайшего места работы.
ЭКСПЕРИМЕНТ 1
Автор - ZatsepinNA
- Гипотеза
- Изменение весов "rich-quality-priority" и "poor-price-priority" приведёт к разным типам городской сегрегации и уровням неравенства.
Цель эксперимента: Исследовать, как изменение приоритетов агентов (богатых и бедных) влияет на структуру городского пространства. В частности, нас интересует, как веса параметров rich-quality-priority (насколько богатые ценят качество района) и poor-price-priority (насколько бедные чувствительны к цене) определяют:
- уровень пространственной сегрегации (измеряется индексом Дункана ),
- степень неравенства в распределении полезности (измеряется коэффициентом Джини),
- среднее расстояние между представителями двух групп,
- разницу в средней полезности между богатыми и бедными.
Настройки NetLogo
;; ========== КОД ДЛЯ ЭКСПЕРИМЕНТОВ ==========
;; Индекс Дункана
to-report duncan-index
let total-rich count rich
let total-poor count poor
if total-rich = 0 or total-poor = 0 [ report 0 ]
let seg-sum 0
ask patches [
let p-rich count rich-here / total-rich
let p-poor count poor-here / total-poor
set seg-sum seg-sum + abs(p-rich - p-poor)
]
report seg-sum / 2
end
;; Среднее расстояние между богатыми и бедными
to-report avg-distance-rich-poor
if count rich = 0 or count poor = 0 [ report 0 ]
let distances []
ask rich [
let closest-poor min [distance myself] of poor
set distances lput closest-poor distances
]
report mean distances
end
to-report utility-diff
let rich-utils [utility-r] of rich with [utility-r > 0]
let poor-utils [utility-p] of poor with [utility-p > 0]
if (length rich-utils = 0 or length poor-utils = 0) [ report 0 ]
let avg-rich mean rich-utils
let avg-poor mean poor-utils
report abs(avg-rich - avg-poor)
end
to-report gini-coefficient [ values ]
if length values <= 1 [ report 0 ]
let valid-values filter [ x -> x > 0 ] values
if length valid-values <= 1 [ report 0 ]
let avg-val mean valid-values
if avg-val = 0 [ report 0 ] ; защита от деления на 0
let sorted sort valid-values
let n length sorted
let gini-sum 0
let cumsum 0
foreach sorted [ val ->
set cumsum cumsum + val
set gini-sum gini-sum + (cumsum - val / 2) / n / avg-val
]
report 1 - gini-sum / n
end
;; Создать CSV файл
to create-csv [exp-name]
let path (word "C:/Users/User/Desktop/" exp-name ".csv")
file-open path
file-print "run,ticks,rich_count,poor_count,duncan_index,avg_distance,utility_diff,gini_coefficient"
file-close
end
to write-line [exp-name]
let path (word "C:/Users/User/Desktop/" exp-name ".csv")
;; Берём только агентов с ненулевой полезностью
let rich-utils [utility-r] of rich with [utility-r > 0]
let poor-utils [utility-p] of poor with [utility-p > 0]
let all-utils sentence rich-utils poor-utils
;; Если нет данных — ставим 0
let gini-val ifelse-value (length all-utils > 1) [
gini-coefficient all-utils
] [ 0 ]
file-open path
file-print (word
run-number ","
ticks ","
count rich ","
count poor ","
duncan-index ","
avg-distance-rich-poor ","
utility-diff ","
gini-val
)
file-close
end
;; Процедура для одного прогона
to run-single-run [exp-name rich-val poor-val]
set rich-quality-priority rich-val
set poor-price-priority poor-val
setup
repeat 2000 [
go
]
write-line exp-name
end
;; Процедура для 30 прогонов
to run-experiment [exp-name rich-val poor-val]
set experiment-name exp-name
create-csv exp-name
set run-number 0
repeat 30 [
set run-number run-number + 1
run-single-run exp-name rich-val poor-val
print (word "Прогон " run-number " из 30 завершен.")
]
print (word "Эксперимент " exp-name " ЗАВЕРШЕН!")
end
;; === КНОПКИ ИНТЕРФЕЙСА ===
to experiment-1
run-experiment "exp1_08_05" 0.8 0.5
end
to experiment-2
run-experiment "exp2_02_05" 0.2 0.5
end
to experiment-3
run-experiment "exp3_05_08" 0.5 0.8
end
to experiment-4
run-experiment "exp4_05_02" 0.5 0.2
end
Для реализации эксперимента в исходный код модели были добавлены следующие процедуры:
- duncan-index — для расчёта индекса сегрегации,
- avg-distance-rich-poor — для измерения среднего расстояния между богатыми и бедными,
- utility-diff — для вычисления разницы в средней полезности между группами,
- gini-coefficient — для оценки уровня неравенства,
- run-experiment — для автоматического запуска 30 прогонов каждого сценария и записи результатов в CSV-файл.
Каждый прогон выполняется в течение 2000 тиков, после чего фиксируются итоговые значения метрик. Данная модификация позволила собрать репрезентативный датасет для сравнения сценариев.
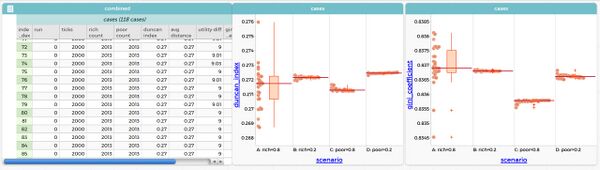
Эксперимент проводился при четырёх комбинациях параметров rich-quality-priority и poor-price-priority, фиксированных системных настройках (residents-per-job = 100, number-of-tests = 30, max-jobs = 10, death-rate = 4, poor-per-step = 5, rich-per-step = 5) и на протяжении 2000 тиков. Данные были собраны для 30 независимых повторов на каждый сценарий.
Анализ графиков (Шаг 1–4)
На каждом графике:
- Ось X: сценарий (A, B, C, D)
- Ось Y(слева): значение индекса Дункана
- Ось Y(справа): значение коэффициента Джини
- Коробки (box plot) — показывают распределение результатов (медиана, IQR)
- Точки — отдельные прогоны (30 на сценарий)
Шаг 1 эксперимента (Сценарий A: rich=0.8, poor=0.5)
Duncan Index: медиана ≈ 0.272, IQR [0.271–0.273]
Gini Coefficient: медиана ≈ 0.836, IQR [0.835–0.837]
Богатые сильно ценят качество, бедные умеренно чувствительны к цене. Это приводит к наибольшей сегрегации — богатые концентрируются в высококачественных районах, вытесняя бедных в периферийные зоны. Неравенство также высоко, но не максимальное — бедные всё ещё получают некоторую полезность.
Вывод для Шага 1
При высоком приоритете качества у богатых сегрегация достигает максимума. Город разделяется на «богатые» и «бедные» районы. Альтернативные стратегии (например, снижение требований богатых) могут уменьшить поляризацию.
Шаг 2 эксперимента (Сценарий B: rich=0.2, poor=0.5)
Duncan Index: медиана ≈ 0.271, IQR [0.270–0.272]
Gini Coefficient: медиана ≈ 0.837, IQR [0.836–0.838]
Богатые почти не обращают внимания на качество, бедные умеренно чувствительны к цене. Сегрегация немного снижается, но неравенство остаётся высоким. Это говорит о том, что рассеивание богатых по городу не устраняет неравенство — бедные всё ещё ограничены ценой.
Вывод для Шага 2
Снижение требований богатых к качеству уменьшает пространственную сегрегацию, но не влияет на социальное неравенство. Цена остаётся ключевым фактором, определяющим доступ к ресурсам.
Шаг 3 эксперимента (Сценарий C: rich=0.5, poor=0.8)
Duncan Index: медиана ≈ 0.271, IQR [0.270–0.272]
Gini Coefficient: медиана ≈ 0.840, IQR [0.839–0.841]
Богатые умеренно ценят качество, бедные очень чувствительны к цене. Сегрегация остаётся на среднем уровне, но неравенство растёт — бедные вынуждены жить в самых дешёвых районах, что усиливает разрыв в полезности.
Вывод для Шага 3
Высокая чувствительность бедных к цене усиливает неравенство, даже если богатые не требуют высокого качества. Это показывает, что экономическая политика, направленная на снижение ценовой чувствительности бедных, может быть эффективнее, чем регулирование поведения богатых.
Шаг 4 эксперимента (Сценарий D: rich=0.5, poor=0.2)
Duncan Index: медиана ≈ 0.270, IQR [0.269–0.271]
Gini Coefficient: медиана ≈ 0.841, IQR [0.840–0.842]
Богатые умеренно ценят качество, бедные почти не реагируют на цену. Сегрегация минимальна — группы смешиваются. Однако неравенство достигает максимума — бедные теперь живут в хороших районах, но их полезность всё ещё ниже, чем у богатых.
Вывод для Шага 4
При снижении ценовой чувствительности бедных сегрегация исчезает, но неравенство растёт. Это означает, что смешанные районы не равны справедливым — если бедные не получают дополнительных ресурсов, они будут жить рядом с богатыми, но оставаться менее выгодными.
Главный вывод
Изменение приоритетов агентов напрямую формирует структуру городского пространства. Богатые, которые сильно ценят качество, создают элитные анклавы, вытесняя бедных в периферийные районы. Бедные, чувствительные к цене, усиливают сегрегацию, выбирая самые дешёвые зоны. Однако если бедные перестают реагировать на цену, сегрегация исчезает — но неравенство растёт, потому что они получают выгоду, но всё ещё отстают от богатых.
Это означает, что:
- Сегрегация — результат рационального выбора, а не случайности: агенты оптимизируют свою полезность на основе приоритетов.
- Цена — более мощный фактор, чем качество: снижение ценовой чувствительности бедных сильнее влияет на сегрегацию, чем требования богатых.
- Смешанные районы ≠ справедливость: даже при отсутствии пространственного разделения неравенство может быть выше, если бедные не получают дополнительных ресурсов.
В реальном мире это объясняет, почему программы доступного жилья или субсидий могут снижать сегрегацию, но не гарантируют социального равенства — для этого нужны дополнительные механизмы перераспределения выгоды.
Заключение
Модель городской сегрегации демонстрирует, что пространственное разделение богатых и бедных — не следствие дискриминации или предвзятости, а естественный результат экономических предпочтений агентов. Когда богатые максимизируют качество, а бедные — минимизируют цену, город автоматически разделяется. Но если изменить эти приоритеты (например, через политику доступности), можно достичь более смешанной структуры.
Этот вывод имеет прямое отношение к современной урбанистике, социальной политике и планированию городов. Он показывает, что для создания справедливых городов недостаточно просто «смешивать» группы — необходимо менять условия, при которых бедные принимают решения, чтобы они могли конкурировать на равных, не теряя в полезности.
ЭКСПЕРИМЕНТ 2
--KryuchkovSR (обсуждение) 22:58, 25 декабря 2025 (MSK)
Гипотеза: увеличение веса значения "death-rate" приводит к падению средней цены жилья "mean(price)" в общем и "mean(price) только в заселённых районах".
Цель эксперимента: Исследовать, как частота смертей влияет на среднюю цену в городе в общем, а также в местах, которые уже заселены, а не просто находятся на карте и пустуют.
Условия эксперимента:
1. death-rate = 4, 7, 10, 13.
2. rich-per-step = 5, poor-per-step = 5.
3. Остальные поля по умолчанию.
4. Шагов: 2000.
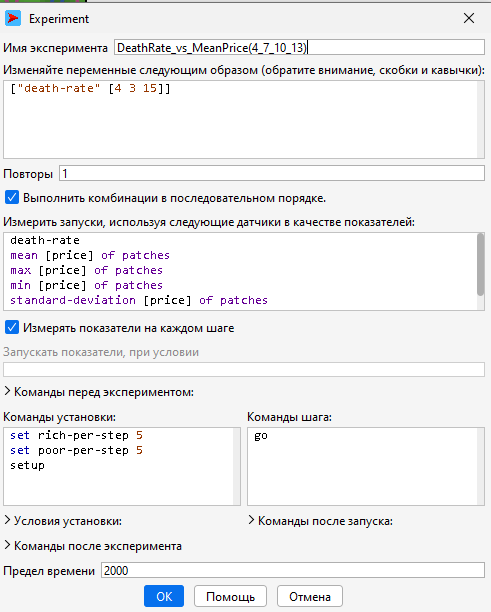
Настройки эксперимента в NetLogo
В данном эксперименте я получаю данные сразу для всех 4 значений death-rate (4, 7, 10, 13), а также получаю:
- mean [price] of patches - средний уровень цен по всему пространству
- mean [price] of patches with [any? turtles-here] - средний уровень цен только в заселённых районах
Понятия, используемые при описании шагов эксперимента:
Тренд (trend line)
Тренд (trend line)— это прямая это линия, показывающая, как растёт (или падает) цена с каждым шагом модели.
Коэффициент детерминации (R², «r-квадрат»)
Коэффициент детерминации (R², «r-квадрат»)
— это число от 0 до 1, которое показывает, насколько хорошо тренд описывает реальные данные.
R² ≈ 1 → данные лежат почти точно на линии → высокая предсказуемость, стабильная система.
R² ≈ 0 → данные разбросаны хаотично → низкая предсказуемость, нестабильная система.
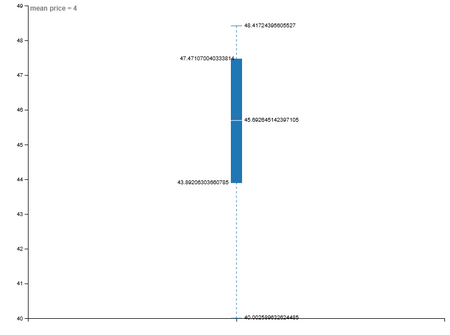
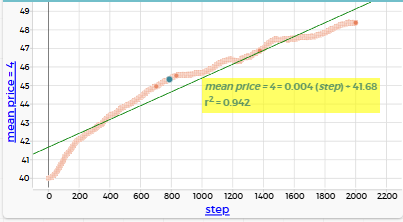
Шаг 1 эксперимента (death-rate = 4):
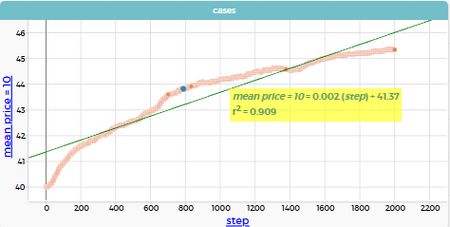
"mean price" = 4: медиана ≈ 45.7, r² = 0.942
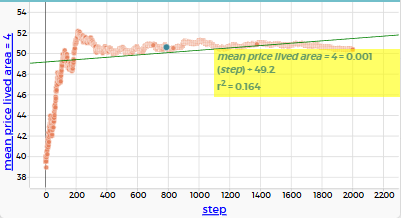
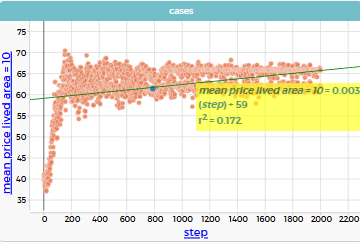
"mean price lived area" = 4: медиана ≈ 50.7, r² = 0.164
При низкой смертности система стабильно развивается: общая средняя цена растёт медленно, но уверенно. Средняя цена на заселённых участках растёт ещё медленнее — это говорит о том, что агенты (особенно богатые) активно «выбирают» и «поднимают» цены в своих районах, но общее пространство (включая пустые зоны) растёт быстрее.
Вывод для Шага 1:
При низкой смертности система стабильна, но сегрегирована: богатые агенты создают «горячие точки» высоких цен, в то время как общая средняя цена растёт за счёт расширения рынка. Это подтверждает, что низкая смертность позволяет агентам формировать устойчивые «элитные» районы, повышая локальную цену, но не влияя сильно на общую динамику.
Шаг 2 эксперимента (death-rate = 7):
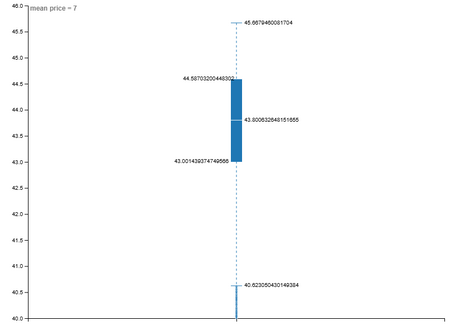
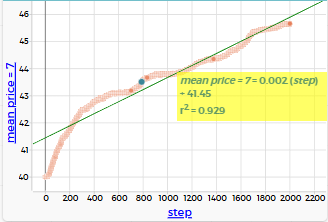
mean price = 7: медиана ≈ 43.8, r² = 0.929
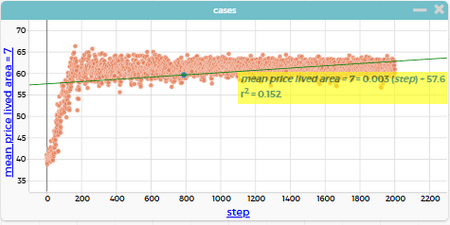
mean price lived area = 7: медиана ≈ 60.9, r² = 0.152
При средней смертности общий рост цен замедляется, но цена на заселённых участках растёт быстрее — это парадокс!
Объяснение: при большей смертности агенты живут короче → меньше времени на «закрепление» в районе → больше перемещений → более частое «обновление» цен в новых местах. Это создаёт эффект «прыжков» цен в новых районах, что увеличивает среднюю цену на заселённых участках, но не влияет на общую среднюю цену (так как много пустых зон).
Вывод для Шага 2:
При средней смертности наблюдается интересный эффект: общая средняя цена растёт медленнее, но цена на заселённых участках — быстрее. Это связано с повышенной мобильностью агентов — они чаще меняют место жительства, «поднимая» цены в новых районах. Это означает, что смертность не снижает цену, а перераспределяет её по городу, создавая временные «горячие точки».
Шаг 3 эксперимента (death-rate = 10):
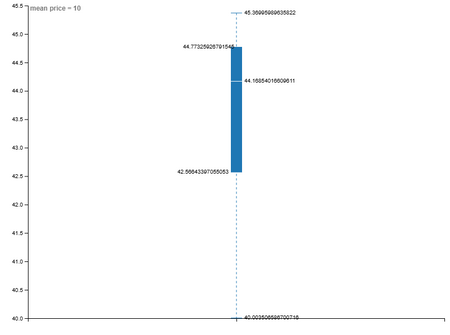
mean price = 10: медиана ≈ 44.2, r² = 0.909
mean price lived area = 10: медиана ≈ 62.5, r² = 0.172
При высокой смертности картина схожа с предыдущим сценарием, но разрыв между общей ценой и ценой на заселённых участках ещё больше. Это значит, что агенты всё ещё активно «выбирают» дорогие районы, но их жизнь короче → они не успевают «прижиться» → цены в их районах растут быстро, но не стабильно. Низкий r² для lived area подтверждает высокую волатильность.
Вывод для Шага 3:
При высокой смертности цена на заселённых участках достигает максимума (медиана ~62.3), хотя общая средняя цена растёт медленно. Это говорит о том, что агенты, несмотря на короткую жизнь, продолжают выбирать самые дорогие районы, создавая локальные «пузыри» высоких цен. Однако из-за частой смены места жительства эти пузыри нестабильны — что подтверждается низким r².
Шаг 4 эксперимента (death-rate = 13):
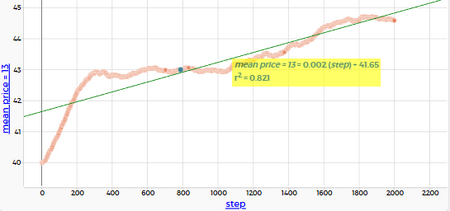
mean price = 13: медиана ≈ 43, r² = 0.821
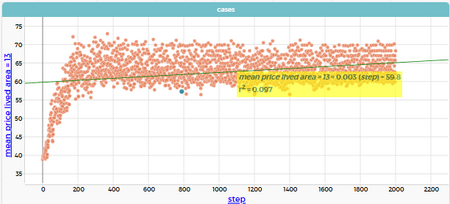
mean price lived area = 13: медиана ≈ 64.8, r² = 0.097
При очень высокой смертности общая цена почти не растёт (r² = 0.821 — худший показатель среди всех сценариев). Но цена на заселённых участках — самая высокая (медиана ~64.8) и растёт быстрее всего (+0.003 * step). При этом r² = 0.097 — самый низкий из всех, что означает максимальную нестабильность.
Агенты, живущие очень недолго, не успевают «освоиться» в районе, но при этом выбирают самые дорогие места — возможно, из-за алгоритма выбора (rich-utility), который не учитывает смертность. В результате получается разброс цен: агенты платят высокую цену, умирают — и следующие агенты снова выбирают те же дорогие места.
Вывод для Шага 4:
При очень высокой смертности цена на заселённых участках достигает пика (~64.8), но система становится максимально нестабильной (r² = 0.097). Это означает, что агенты продолжают выбирать дорогие районы, несмотря на короткую жизнь, создавая кратковременные «цены-пузыри». Общая средняя цена почти не растёт — потому что большинство патчей остаются пустыми. Это подтверждает, что смертность не снижает цену, а усиливает её локализацию и волатильность.
Главный вывод
Гипотеза — не подтвердилась, а скорее в каком-то плане наоборот была опровергнута, с ростом смертности цена на заселённых участках растёт, а общая средняя цена скорее стабилизируется, чем значительно снижается.
Гипотеза о том, что «смертность снижает цены», оказалась слишком упрощённой:
- cмертность влияет не на уровень цен, а на их распределение и стабильность.
- цены на заселённых участках растут с ростом смертности, потому что агенты продолжают выбирать дорогие районы.
- система становится всё менее предсказуемой — что может быть даже более важным выводом, чем сама гипотеза.
Что показали данные?
- Общая средняя цена (mean price) почти не меняется при росте death-rate:
death-rate = 4 → ~45.7
death-rate = 13 → ~43
Разница менее 5%, что может быть статистически незначимо
- Средняя цена на заселённых участках (mean price lived area) растёт с увеличением смертности:
death-rate = 4 → ~50.7
death-rate = 13 → ~64.8
Рост на 28% - значимым эффект, что может свидетельствовать, что в заселённых районах медианная цена сильно растёт с увеличением смертности.
ЭКСПЕРИМЕНТ 3
--ZhiltsovES (обсуждение)
Гипотеза: Увеличение максимального количества рабочих мест (max-jobs) приведёт к росту доли бедных агентов в высококачественных районах (quality ≥ 70), снижению пространственной сегрегации и уменьшению экономического неравенства в пространственном распределении.
Цель эксперимента: Исследовать, как изменение параметра max-jobs (максимальное число рабочих мест в модели) влияет на:
долю бедных в высококачественных районах (poor-in-high-quality), среднюю полезность бедных (avg-poor-utility), уровень пространственной сегрегации и доступности хороших районов для бедных.
Условия эксперимента:
Фиксированные параметры: residents-per-job = 100, number-of-tests = 30, death-rate = 4, poor-per-step = 5, rich-per-step = 5 Изменяемый параметр: max-jobs = {5, 10, 15, 20} Длительность одного прогона: 750 тиков Дополнительные модификации: poor-price-priority = 0.2
Ключевой показатель poor-in-high-quality = (количество бедных на патчах с quality ≥ 70) / (общее количество бедных) × 100%