Обсуждение:Wealth Distribution

Экспериментальные датасеты NetLogo

Эксперимент 29 ноября 2025

Мы получили набор данных из модели Wealth Distribution - BehaviorSpace со следующими условиями:

["num-grain-grown" 4]
["percent-best-land" 5 10 15 20]
["metabolism-max" 10 15 20]
["max-vision" 4 5 6 7 8 9 10]
["num-people" 400]
["grain-growth-interval" 2]
["life-expectancy-min" 30]
["life-expectancy-max" 70]

В эксперименте собирались следующие метрики:

ticks
count turtles
count turtles with [color = red]
count turtles with [color = green]
count turtles with [color = blue]
gini-index-reserve / num-people
gini-index-reserve

Результаты

• https://raw.githubusercontent.com/patarakin/stat-data/refs/heads/main/datasets/csv/Wealth%20Distribution%20experiment_29-table.csv

График изменения неравенства во времени (gini-index-reserve по ticks)

Malena Buzdugan 11:04, 13 декабря 2025 (MSK)

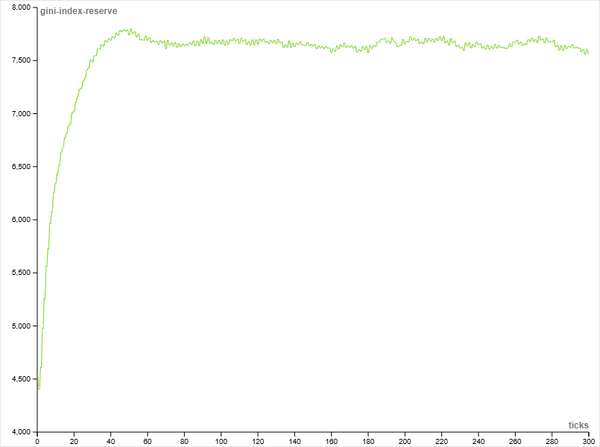
Показывает, как неравенство растёт или стабилизируется во времени. В типичных моделях типа Sugarscape коэффициент Джини быстро растёт в начале (разрыв между «богатыми» и «бедными»), затем стабилизируется.

Сравнение неравенства по max-vision

Malena Buzdugan 11:04, 13 декабря 2025 (MSK)

Чем выше max-vision (способность видеть ресурсы), тем ниже коэффициент Джини — то есть, неравенство уменьшается. Это говорит о том, что доступ к информации (в данном случае — возможность видеть ресурсы) способствует более равному распределению богатства.

График: Динамика численности красных агентов

--Kate (обсуждение) 23:07, 21 декабря 2025 (MSK)

Что показывает: это Streamgraph (потоковый график), который показывает, как меняется количество агентов, окрашенных в красный цвет, в течение симуляции. Цвета слоев (красный, розовый, белый) соответствуют разным значениям параметра max-vision (4, 5, 6). Цифры внутри областей — это значения max-vision.

О чём говорит: Общая тенденция: количество красных агентов в целом растет в начале симуляции, а затем стабилизируется или даже немного снижается. Это говорит о том, что красный цвет, обозначающий агентов с определенным статусом (например, "богатые" или "активные"), вначале доминирует, но потом доля красных агентов перестает расти.

Сравнение по max-vision: max-vision = 6 (темно-красный): эта группа имеет самую большую площадь под кривой. Это значит, что при более широком "поле зрения" (max-vision=6) агенты чаще становятся "красными". Возможно, они лучше находят ресурсы или взаимодействуют с другими агентами. max-vision = 5 (розовый): промежуточное положение. max-vision = 4 (белый/светло-серый): наименьшая площадь. Агенты с ограниченным полем зрения реже становятся "красными".

Резкое падение индекса Джини около шага 160 совпадает с резким падением численности всех групп красных агентов. Это подтверждает гипотезу: именно "красные" агенты были главными "богачами", и их массовая гибель привела к падению неравенства.

Вывод

Параметр max-vision напрямую влияет на то, насколько успешно агенты могут достичь "красного" статуса. Чем дальше видят агенты, тем больше их становится в этой группе. Резкое падение численности красных агентов коррелирует с обвалом неравенства, что говорит о том, что именно эта группа была источником неравенства.

График: Распределение значений max-vision

Что показывает: это Beeswarm plot (пчелиный рой), где по горизонтальной оси отложены значения параметра max-vision (4, 5, 6), а по вертикальной — значения gini-index-reserve / num-people. Каждая точка — это одно наблюдение (один шаг симуляции).

О чём говорит: Точки четко разделены на три кластера по значению max-vision. Это хорошо визуализирует, что данные сгруппированы по этому параметру. В каждом кластере точки плотно сгруппированы, что говорит о том, что в пределах одного значения max-vision показатель (например, Джини) имеет схожее распределение. Видно, что кластер max-vision = 6 (красный) смещен вправо, а max-vision = 4 (голубой) — влево. Если по вертикали отложен индекс Джини, это означает, что при max-vision = 6 неравенство выше, чем при max-vision = 4.

Вывод:

Этот график наглядно демонстрирует, что параметр max-vision является ключевым фактором, определяющим поведение модели. Разные значения этого параметра приводят к принципиально разным результатам (разному уровню неравенства или доле красных агентов). Он позволяет сравнить "центры тяжести" распределений для разных экспериментов.

Эксперимент 07 декабря 2025 (480 runs)

	Description	KeyDescripions
NetLogo Wealth Distribution 07122025	Датасет выращен при помощи агентов модели NetLogo Wealth Distribution	"run number", percent.best.land - процент лучших земель metabolism.max (уровень метаболизма) max.vision - способности черепах (видение) grain.growth.interval gini - коэффициент Джини (неравенство)

Мы получили набор данных из модели Wealth Distribution - BehaviorSpace со следующими условиями:

["num-grain-grown" 5]
["percent-best-land" 5 10 15 20]
["metabolism-max" 10 15]
["max-vision" 4 6 8 10 12 14]
["num-people" 300]
["grain-growth-interval" 1 2 3 4 5 6 7 8 9 10]
["life-expectancy-min" 30]
["life-expectancy-max" 80]

В эксперименте собирались следующие метрики:

ticks
count turtles
gini-index-reserve / num-people

При этом данные собирались только в конце прогона - 500 ticks

Мы хотели исследовать влияние способностей людей max-vision на неравномерность распределения богатства - коэффициент Джини gini-index-reserve / num-people

Результаты

• https://raw.githubusercontent.com/patarakin/stat-data/refs/heads/main/datasets/csv/Wealth%20Distribution%20experiment_07_12table.csv
• https://raw.githubusercontent.com/patarakin/stat-data/refs/heads/main/datasets/csv/data_model_07_12.csv

Процесс обработки в R

url <- "https://raw.githubusercontent.com/patarakin/stat-data/refs/heads/main/datasets/csv/data_model_07_12.csv"

data_clean <- read.csv(url)

boxplot(gini ~ max.vision, data = data_clean,
        main = "Влияние дальности видения на коэффициент Джини",
        xlab = "Дальность видения (max.vision)",
        ylab = "Коэффициент Джини",
        col = "lightblue")

• boxplot

# Формула: зависимая_переменная ~ независимая_переменная
model_vision <- lm(gini ~ max.vision, data = data_clean)
summary(model_vision)

Call:
lm(formula = gini ~ max.vision, data = data_clean)

bResiduals:
     Min        1Q    Median        3Q       Max 
-0.052899 -0.012218  0.002057  0.011398  0.047757 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept)  0.2348489  0.0022385 104.915  < 2e-16 ***
max.vision  -0.0009564  0.0002325  -4.113  4.6e-05 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.0174 on 478 degrees of freedom
Multiple R-squared:  0.03418,	Adjusted R-squared:  0.03216 
F-statistic: 16.92 on 1 and 478 DF,  p-value: 4.601e-05

Визуализация эксперимента

--Григорий Глаголенко (обсуждение) 00:05, 22 декабря 2025 (MSK)

Boxplot

	Description
Boxplot	Boxplot (диаграмма размаха, ящик с усами) — это графический метод визуализации распределения количественных данных через их квартили. Этот тип диаграммы позволяет быстро оценить центральную тенденцию, вариабельность и асимметрию данных, а также выявить аномальные значения (выбросы). Boxplot показывает сразу 5 ключевых статистик (минимум, Q1, медиана, Q3, максимум) + выбросы.

[[Файл:Боксплот.png|300px]
Сравнение медиан: медианы (горизонтальные линии) для разных групп довольно близки друг к другу, что говорит о том, что средний уровень неравенства примерно одинаков при разных значениях параметра.

Разброс данных: заметно, что высота ящиков (IQR) и длина усов различаются. Это означает, что разброс (дисперсия) значений индекса Джини меняется в зависимости от параметра. Например, группа с параметром 4 имеет более широкий IQR, чем группа с параметром 6, что указывает на большую вариативность результатов в первой группе.

Наличие выбросов: в каждой группе есть множество выбросов (точки). Это может указывать на то, что модель иногда выдает экстремально высокие или низкие значения неравенства, независимо от параметра.

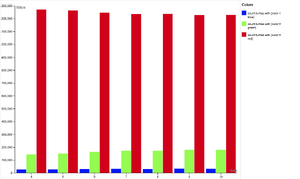
Multi-set bar chart

Доминирование "богатых" (red): в подавляющем большинстве экспериментов (более 80% от общего числа count turtles) агенты находятся в состоянии red. Это означает, что модель стабильно приводит к ситуации, где большинство ресурсов сосредоточено в руках небольшой группы "богатых" агентов.

Малочисленность "бедных" (blue): количество агентов с цветом red крайне мало (обычно менее 5-7% от общего числа). Это указывает на то, что крайняя нищета или полное обнищание (исчезновение) затрагивает лишь небольшую часть популяции.

Среднее состояние (green) — промежуточное: группа green занимает промежуточное положение по численности (около 10-15%). Это говорит о том, что есть определенная прослойка "среднего класса", но она значительно меньше, чем "богатые".

Устойчивость к параметрам: как видно из графика Multi-set bar chart, соотношение между цветами практически не меняется при изменении ключевого параметра max-vision. Это свидетельствует о том, что наблюдаемое неравенство является фундаментальной чертой модели, а не следствием конкретного значения этого параметра. Модель стабильно воспроизводит эту структуру распределения независимо от того, насколько далеко могут видеть агенты.