Обсуждение:Wealth Distribution
Экспериментальные датасеты NetLogo
Эксперимент 29 ноября 2025
Мы получили набор данных из модели Wealth Distribution - BehaviorSpace со следующими условиями:
["num-grain-grown" 4] ["percent-best-land" 5 10 15 20] ["metabolism-max" 10 15 20] ["max-vision" 4 5 6 7 8 9 10] ["num-people" 400] ["grain-growth-interval" 2] ["life-expectancy-min" 30] ["life-expectancy-max" 70]
В эксперименте собирались следующие метрики:
ticks count turtles count turtles with [color = red] count turtles with [color = green] count turtles with [color = blue] gini-index-reserve / num-people gini-index-reserve
- Результаты
График изменения неравенства во времени (gini-index-reserve по ticks)
Malena Buzdugan 11:04, 13 декабря 2025 (MSK)
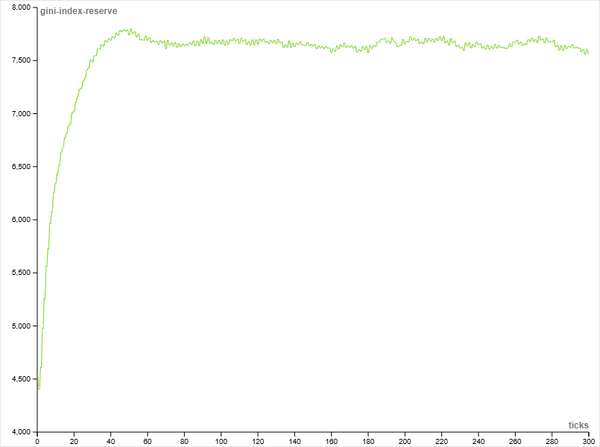
Показывает, как неравенство растёт или стабилизируется во времени. В типичных моделях типа Sugarscape коэффициент Джини быстро растёт в начале (разрыв между «богатыми» и «бедными»), затем стабилизируется.
Сравнение неравенства по max-vision
Malena Buzdugan 11:04, 13 декабря 2025 (MSK)

Чем выше max-vision (способность видеть ресурсы), тем ниже коэффициент Джини — то есть, неравенство уменьшается. Это говорит о том, что доступ к информации (в данном случае — возможность видеть ресурсы) способствует более равному распределению богатства.
График: Динамика численности красных агентов
--Kate (обсуждение) 23:07, 21 декабря 2025 (MSK)

Что показывает: это Streamgraph (потоковый график), который показывает, как меняется количество агентов, окрашенных в красный цвет, в течение симуляции. Цвета слоев (красный, розовый, белый) соответствуют разным значениям параметра max-vision (4, 5, 6). Цифры внутри областей — это значения max-vision.
О чём говорит: Общая тенденция: количество красных агентов в целом растет в начале симуляции, а затем стабилизируется или даже немного снижается. Это говорит о том, что красный цвет, обозначающий агентов с определенным статусом (например, "богатые" или "активные"), вначале доминирует, но потом доля красных агентов перестает расти.
Сравнение по max-vision: max-vision = 6 (темно-красный): эта группа имеет самую большую площадь под кривой. Это значит, что при более широком "поле зрения" (max-vision=6) агенты чаще становятся "красными". Возможно, они лучше находят ресурсы или взаимодействуют с другими агентами. max-vision = 5 (розовый): промежуточное положение. max-vision = 4 (белый/светло-серый): наименьшая площадь. Агенты с ограниченным полем зрения реже становятся "красными".
Резкое падение индекса Джини около шага 160 совпадает с резким падением численности всех групп красных агентов. Это подтверждает гипотезу: именно "красные" агенты были главными "богачами", и их массовая гибель привела к падению неравенства.
Вывод
Параметр max-vision напрямую влияет на то, насколько успешно агенты могут достичь "красного" статуса. Чем дальше видят агенты, тем больше их становится в этой группе. Резкое падение численности красных агентов коррелирует с обвалом неравенства, что говорит о том, что именно эта группа была источником неравенства.
График: Распределение значений max-vision

Что показывает: это Beeswarm plot (пчелиный рой), где по горизонтальной оси отложены значения параметра max-vision (4, 5, 6), а по вертикальной — значения gini-index-reserve / num-people. Каждая точка — это одно наблюдение (один шаг симуляции).
О чём говорит: Точки четко разделены на три кластера по значению max-vision. Это хорошо визуализирует, что данные сгруппированы по этому параметру. В каждом кластере точки плотно сгруппированы, что говорит о том, что в пределах одного значения max-vision показатель (например, Джини) имеет схожее распределение. Видно, что кластер max-vision = 6 (красный) смещен вправо, а max-vision = 4 (голубой) — влево. Если по вертикали отложен индекс Джини, это означает, что при max-vision = 6 неравенство выше, чем при max-vision = 4.
Вывод:
Этот график наглядно демонстрирует, что параметр max-vision является ключевым фактором, определяющим поведение модели. Разные значения этого параметра приводят к принципиально разным результатам (разному уровню неравенства или доле красных агентов). Он позволяет сравнить "центры тяжести" распределений для разных экспериментов.
Эксперимент 07 декабря 2025 (480 runs)
| Description | KeyDescripions | |
|---|---|---|
| NetLogo Wealth Distribution 07122025 | Датасет выращен при помощи агентов модели NetLogo Wealth Distribution |
|
Мы получили набор данных из модели Wealth Distribution - BehaviorSpace со следующими условиями:
["num-grain-grown" 5] ["percent-best-land" 5 10 15 20] ["metabolism-max" 10 15] ["max-vision" 4 6 8 10 12 14] ["num-people" 300] ["grain-growth-interval" 1 2 3 4 5 6 7 8 9 10] ["life-expectancy-min" 30] ["life-expectancy-max" 80]
В эксперименте собирались следующие метрики:
ticks count turtles gini-index-reserve / num-people
При этом данные собирались только в конце прогона - 500 ticks
Мы хотели исследовать влияние способностей людей max-vision на неравномерность распределения богатства - коэффициент Джини gini-index-reserve / num-people
- Результаты
- https://raw.githubusercontent.com/patarakin/stat-data/refs/heads/main/datasets/csv/Wealth%20Distribution%20experiment_07_12table.csv
- https://raw.githubusercontent.com/patarakin/stat-data/refs/heads/main/datasets/csv/data_model_07_12.csv
Процесс обработки в R
url <- "https://raw.githubusercontent.com/patarakin/stat-data/refs/heads/main/datasets/csv/data_model_07_12.csv"
data_clean <- read.csv(url)
boxplot(gini ~ max.vision, data = data_clean,
main = "Влияние дальности видения на коэффициент Джини",
xlab = "Дальность видения (max.vision)",
ylab = "Коэффициент Джини",
col = "lightblue")
# Формула: зависимая_переменная ~ независимая_переменная
model_vision <- lm(gini ~ max.vision, data = data_clean)
summary(model_vision)
Call: lm(formula = gini ~ max.vision, data = data_clean)
bResiduals:
Min 1Q Median 3Q Max
-0.052899 -0.012218 0.002057 0.011398 0.047757
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.2348489 0.0022385 104.915 < 2e-16 ***
max.vision -0.0009564 0.0002325 -4.113 4.6e-05 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.0174 on 478 degrees of freedom Multiple R-squared: 0.03418, Adjusted R-squared: 0.03216 F-statistic: 16.92 on 1 and 478 DF, p-value: 4.601e-05
Визуализация эксперимента
--Григорий Глаголенко (обсуждение) 00:05, 22 декабря 2025 (MSK)
Boxplot
| Description | |
|---|---|
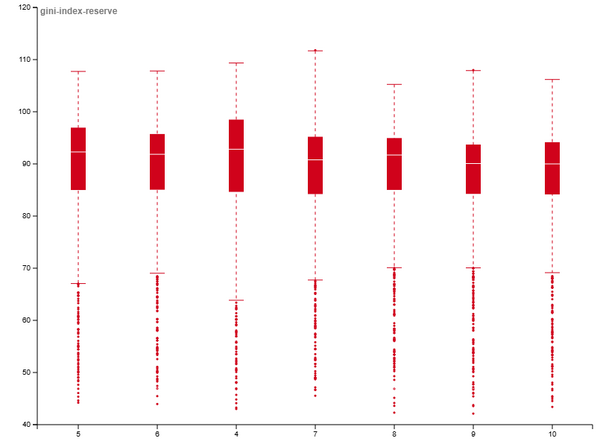
| Boxplot | Boxplot (диаграмма размаха, ящик с усами) — это графический метод визуализации распределения количественных данных через их квартили. Этот тип диаграммы позволяет быстро оценить центральную тенденцию, вариабельность и асимметрию данных, а также выявить аномальные значения (выбросы). Boxplot показывает сразу 5 ключевых статистик (минимум, Q1, медиана, Q3, максимум) + выбросы. |
Сравнение медиан: медианы (горизонтальные линии) для разных групп довольно близки друг к другу, что говорит о том, что средний уровень неравенства примерно одинаков при разных значениях параметра.
Разброс данных: заметно, что высота ящиков (IQR) и длина усов различаются. Это означает, что разброс (дисперсия) значений индекса Джини меняется в зависимости от параметра. Например, группа с параметром 4 имеет более широкий IQR, чем группа с параметром 6, что указывает на большую вариативность результатов в первой группе.
Наличие выбросов: в каждой группе есть множество выбросов (точки). Это может указывать на то, что модель иногда выдает экстремально высокие или низкие значения неравенства, независимо от параметра.
Multi-set bar chart
Доминирование "бедных" (red): в подавляющем большинстве экспериментов (более 80% от общего числа count turtles) агенты находятся в состоянии red. Это означает, что модель стабильно приводит к ситуации, где большинство ресурсов сосредоточено в руках небольшой группы "богатых" агентов.
Малочисленность "богатых" (blue): количество агентов с цветом red крайне мало (обычно менее 5-7% от общего числа). Это указывает на то, что крайняя нищета или полное обнищание (исчезновение) затрагивает большую часть популяции.
Среднее состояние (green) — промежуточное: группа green занимает промежуточное положение по численности (около 10-15%). Это говорит о том, что есть определенная прослойка "среднего класса", но она значительно меньше, чем "богатые".
Устойчивость к параметрам: как видно из графика Multi-set bar chart, соотношение между цветами практически не меняется при изменении ключевого параметра max-vision. Это свидетельствует о том, что наблюдаемое неравенство является фундаментальной чертой модели, а не следствием конкретного значения этого параметра. Модель стабильно воспроизводит эту структуру распределения независимо от того, насколько далеко могут видеть агенты.
Визуализация эксперимента
--Хлебова Екатерина (обсуждение)
Parallel coordinates

Данный параллельный координатный график отображает многомерный анализ модели распределения богатства. Каждая линия на графике представляет одну симуляцию (одну комбинацию параметров), а вертикальные оси соответствуют пяти параметрам модели: процент лучших земель (percent.best.land), максимальный метаболизм (metabolism.max), радиус видимости агентов (max.vision), интервал восстановления зерна (grain.growth.interval) и итоговый коэффициент Джини (gini). Все линии имеют серый цвет, что позволяет оценить общие тенденции и кластеры без цветового кодирования.
График позволяет выявить комплексные взаимосвязи между параметрами модели. Наиболее выраженные паттерны наблюдаются на оси max.vision — заметно, что линии, соответствующие высоким значениям коэффициента Джини (верхняя часть последней оси), чаще проходят через высокие значения радиуса видимости (10-14). Также наблюдается кластеризация на оси grain.growth.interval: многие линии сходятся в районе средних значений (4-7), что соответствует наиболее частым сценариям модели.
Анализ паттернов:
- Высокое неравенство (значения gini > 0.25): ассоциируется с комбинациями, где max.vision ≥ 10 и grain.growth.interval между 4 и 7.
- Низкое неравенство (значения gini < 0.20): чаще встречается при низком max.vision (4-6) в сочетании с экстремальными значениями grain.growth.interval (1-2 или 9-10).
- Роль других параметров: percent.best.land и metabolism.max показывают более равномерное распределение линий, что указывает на их меньшую детерминирующую роль по сравнению с max.vision.
Особенности распределения на оси grain.growth.interval: на этой оси наблюдается наибольшая концентрация линий в диапазоне 4-7. Такое сгущение объясняется тем, что средние значения интервала восстановления ресурсов (4-7 тактов) создают оптимальные условия для формирования неравенства. При очень быстром восстановлении (1-2) ресурсы доступны всем агентам равномерно, что снижает преимущество более "зрячих" агентов. При очень медленном восстановлении (9-10) ресурсов становится настолько мало, что даже агенты с высоким зрением не могут накопить существенное преимущество. Именно средние значения позволяют агентам с высоким max.vision эффективно монополизировать ресурсы и создать устойчивое неравенство.
Плотность линий как индикатор вероятности: высокая плотность линий в определённых диапазонах grain.growth.interval указывает на то, что эти значения параметра наиболее часто приводят к реалистичным сценариям в модели. Экстремальные значения (1-2 и 9-10) имеют значительно меньше линий, что соответствует менее вероятным или менее устойчивым конфигурациям системы.
Подтверждается базовый принцип модели — агенты с большей "видимостью" получают систематическое преимущество. Интересный инсайт: максимальное неравенство возникает не при самой быстрой доступности ресурсов (grain.growth.interval = 1), а при средней скорости восстановления, создавая условия для устойчивого накопления преимущества.
Вывод: экономическое неравенство в модели Wealth Distribution формируется под комплексным влиянием параметров, где ключевую роль играет доступ к информации (max.vision), а динамика ресурсов (grain.growth.interval) выступает как модулирующий фактор. Серый цвет всех линий подчеркивает плотность распределения комбинаций параметров и позволяет увидеть, какие траектории чаще всего приводят к разным уровням неравенства.
| Параметр | Диапазон значений | Описание |
|---|---|---|
| percent.best.land | 5-20 | Процент лучших земель (ресурсов) в экономике |
| metabolism.max | 10-15 | Максимальный метаболизм агентов (потребление зерна за такт) |
| max.vision | 4-14 | Радиус видимости агентов для поиска ресурсов |
| grain.growth.interval | 1-10 | Интервал восстановления зерна на участках |
| gini | 0.18-0.27 | Коэффициент Джини (уровень экономического неравенства) |
Bumpchart

Bumpchart демонстрирует изменение ранга влиятельности разных уровней зрения агентов (max.vision) на экономическое неравенство в зависимости от интервала восстановления ресурсов (grain.growth.interval). По горизонтальной оси отложены значения grain.growth.interval (1-10), по вертикальной — ранги от 1 (самое сильное влияние) до 6 (самое слабое влияние). Каждая цветная линия представляет один уровень max.vision (4, 6, 8, 10, 12, 14).
График показывает, как "важность" разных типов агентов меняется при изменении скорости экономического обновления.
Ключевые паттерны:
- Стабильное доминирование высокого зрения: Линия max.vision=14 (тёмная) почти всегда занимает высшие ранги (1-2 позиции), что означает, что агенты с максимальным зрением оказывают наибольшее влияние на неравенство практически при всех скоростях восстановления ресурсов.
- Динамика средних значений зрения: Линии max.vision=10 и 12 демонстрируют интересную динамику:
- При очень быстром восстановлении (interval 1-2) они занимают средние позиции
- При interval 3-7 поднимаются в топ-3
- При interval 8-10 снова опускаются
- Низкое зрение — стабильно слабое влияние: Линии max.vision=4 и 6 почти всегда находятся в нижней части графика (ранги 5-6), подтверждая, что агенты с ограниченным зрением мало влияют на формирование неравенства.
- Критический перелом при interval=3: На графике виден резкий "перелом" большинства линий при grain.growth.interval=3. Это указывает на пороговое значение, после которого влияние зрения на неравенство качественно меняется.
- Сходимость при экстремальных значениях: При interval=1 (очень быстрый рост) и interval=10 (очень медленный рост) линии сближаются, что означает выравнивание влияния разных типов агентов в экстремальных экономических условиях.
Интерпретация ранжирования: Чем выше расположена линия на графике, тем сильнее агенты с данным уровнем зрения влияют на итоговое неравенство. Например, при interval=5:
- 1 место: vision=14 (самое сильное влияние)
- 2 место: vision=12
- 3 место: vision=8
- 4 место: vision=10
- 5 место: vision=6
- 6 место: vision=4 (самое слабое влияние)
Сравнение с предыдущими анализами: Bumpchart подтверждает выводы из Parallel coordinates и Beeswarm plot о ключевой роли max.vision, но добавляет важный нюанс — показывает не абсолютное значение влияния, а относительное ранжирование. График демонстрирует, что даже при изменении экономических условий (grain.growth.interval) иерархия влияния по зрению в целом сохраняется.
Вывод: Bumpchart наглядно показывает, что параметр max.vision является системообразующим фактором неравенства в модели. Агенты с высоким зрением (10-14) стабильно доминируют в формировании неравенства при большинстве экономических условий, в то время как влияние агентов с низким зрением минимально. Однако график также выявляет нелинейность: при экстремальных значениях grain.growth.interval (1 и 10) различия в влиянии сглаживаются, что соответствует экономической интуиции — в условиях кризиса или сверхбыстрого роста индивидуальные преимущества становятся менее значимыми.
| Ось/Элемент | Параметр | Объяснение |
|---|---|---|
| X-Axis | grain.growth.interval | Интервал восстановления ресурсов (1-10 тактов) |
| Y-Axis | Ранг влияния | Позиция от 1 (самое сильное влияние) до 6 (самое слабое) |
| Lines | max.vision | Уровень зрения агентов: 4, 6, 8, 10, 12, 14 |
| Цвет линий | max.vision | Разные оттенки синего для разных уровней зрения |
Методология ранжирования: Для каждого значения grain.growth.interval рассчитывается средний коэффициент Джини для каждого уровня max.vision, затем эти средние значения ранжируются от наибольшего к наименьшему. Высокий ранг = высокое среднее gini = сильное влияние на неравенство.
Визуализация эксперимента
--PanshinaZina (обсуждение) 17:12, 25 декабря 2025 (MSK)
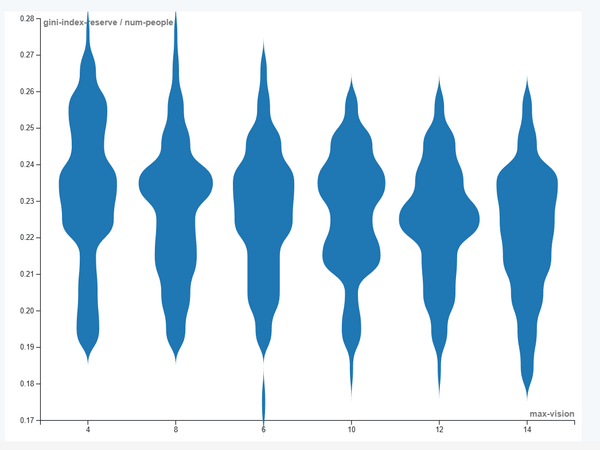
Violin Plot
В рамках исследования влияния параметров модели Wealth Distribution на социально-экономическое неравенство был проведён эксперимент с фокусом на способности агентов видеть ресурсы (max-vision). Для визуализации распределения нормированного коэффициента Джини (gini-index-reserve / num-people) в зависимости от различных уровней зрения был построен Violin Plot. Этот тип графика был выбран для отображения не только средних тенденций, но и полной картины распределения данных, включая плотность вероятности, разброс значений и потенциальные модальности.
На оси X были расположены категориальные значения max-vision (4, 6, 8, 10, 12, 14), а на оси Y — соответствующие значения коэффициента Джини.
Данный график наглядно демонстрирует, что влияние параметра max-vision на неравенство носит неоднозначный и нелинейный характер. При минимальном значении зрения (4) распределение коэффициента Джини узкое и сконцентрировано в районе значений 0.195–0.205. Это указывает на режим стабильно низкого неравенства, вероятно, потому что ограниченные способности агентов не позволяют им эффективно находить и накапливать ресурсы, что приводит к условному «равенству в бедности».
Наиболее показательной является эволюция формы распределения при переходе к max-vision = 6 и особенно к max-vision = 8. Распределение не только смещается вверх по шкале неравенства, но и радикально расширяется, приобретая широкую верхнюю часть. Это прямо свидетельствует о двух ключевых процессах: во-первых, средний уровень неравенства растёт, а во-вторых, резко увеличивается вариативность результатов моделирования. Широкая верхняя часть «скрипки» при значении 8 означает, что во многих прогонах модели возникали сценарии с экстремально высоким расслоением. Такая форма говорит о возникновении разделения: в системе с умеренными возможностями начинают чётко выделяться «успешные» агенты, эффективно использующие своё зрение для концентрации ресурсов, и «неуспешные», что и порождает высокий разброс в благосостоянии.
При дальнейшем росте max-vision до 10, 12 и 14 единиц распределение снова сужается и смещается к более низким значениям Джини. Это указывает на то, что сверхвысокие способности действуют как уравнивающий фактор: когда все агенты обладают исчерпывающей информацией о ресурсах, конкурентное преимущество, основанное на зрении, исчезает, и распределение богатства становится снова более компактным и равномерным.
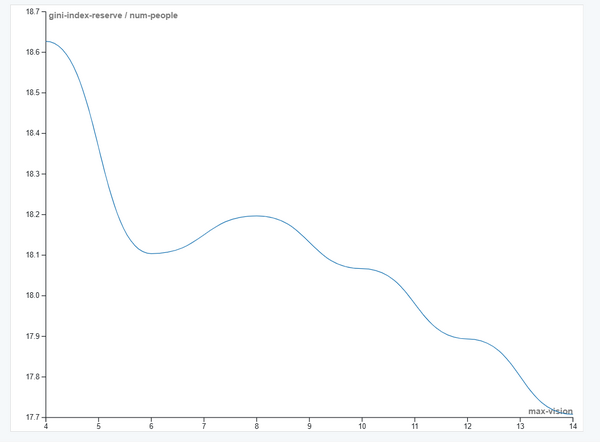
Line Chart
Для дополнения анализа и выявления усреднённой динамики изменений был также построен линейный график (Line Chart), отображающий зависимость среднего значения коэффициента Джини от параметра max-vision.
Линейный график, построенный по усреднённым данным, предоставляет чёткую и однозначную количественную траекторию изменения неравенства в зависимости от возможностей агентов. Кривая имеет ярко выраженную форму перевёрнутой буквы «U», что является статистическим свидетельством наличия порогового или оптимального эффекта. Начальный отрезок графика, от max-vision=4 до max-vision=8, демонстрирует устойчивый и почти линейный рост коэффициента Джини с приблизительно 0.195 до пикового значения около 0.265. Этот восходящий тренд можно интерпретировать как фазу нарастания конкурентного дифференциала: каждый прирост в способности видеть ресурсы даёт агентам всё большее преимущество для их опережающего захвата. В этой зоне улучшение индивидуальных возможностей напрямую конвертируется в усиление социального расслоения, так как выгоду от них получают не все агенты равномерно.
Ключевой точкой графика является вершина кривой при max-vision=8. Это значение выступает своеобразной «точкой перелома» или максимумом неравенства в системе. После её достижения динамика кардинально меняется: дальнейшее увеличение зрения до 10, 12 и 14 единиц приводит не к росту, а к последовательному и монотонному снижению коэффициента Джини. Кривая опускается с пика в 0.265 до уровня около 0.185, что даже ниже исходной точки при минимальном зрении. Нисходящая ветвь графика указывает на то, что после преодоления определённого порога расширение возможностей начинает работать в противоположном направлении — как механизм снижения неравенства. Это можно объяснить переходом от режима конкурентного преимущества к режиму всеобщей доступности: когда зрение становится исключительно высоким, ресурсное пространство становится «прозрачным» для всей популяции. Исчезает сама основа для дифференциации — информационная асимметрия, — и агенты с разными исходными данными получают практически равные шансы на поиск и сбор ресурсов, что и приводит к выравниванию распределения благ. Таким образом, график не просто фиксирует усреднённую зависимость, а визуализирует фундаментальный сдвиг в качестве воздействия параметра max-vision на социальную динамику модели.
Общие выводы по результатам анализа графиков
Совместное рассмотрение Violin Plot и Line Chart позволяет сделать содержательный вывод о сложном, нелинейном характере влияния способностей агентов на социальное неравенство в модели. Violin Plot показывает, что наибольший разброс значений и экстремальные уровни неравенства наблюдаются именно при промежуточных значениях max-vision (6–8), что свидетельствует о высокой нестабильности и вариативности исходов в этом диапазоне. Line Chart, в свою очередь, чётко фиксирует точку максимума неравенства при max-vision=8 и последующий спад. Это согласованное поведение двух графиков указывает на то, что в смоделированной системе существует оптимальный — с точки зрения генерации неравенства — уровень возможностей агентов. Умеренные способности создают условия для формирования конкурентных преимуществ и резкой дифференциации, тогда как как низкие, так и очень высокие возможности приводят к более равномерному и предсказуемому распределению ресурсов.