Как провести регрессионный анализ: различия между версиями
Материал из Поле цифровой дидактики
Patarakin (обсуждение | вклад) |
Patarakin (обсуждение | вклад) Нет описания правки |
||
| (не показано 5 промежуточных версий этого же участника) | |||
| Строка 3: | Строка 3: | ||
|Field_of_knowledge=Статистика, Моделирование | |Field_of_knowledge=Статистика, Моделирование | ||
|Возрастная категория=16 | |Возрастная категория=16 | ||
|similar_concepts=МНК, | |similar_concepts=МНК, Регрессия, Коэффициент корреляции | ||
|Environment=CORGIS, CODAP, RAWGraphs, StatKey | |||
}} | }} | ||
== Датасет [[CORGIS]] == | == Датасет [[CORGIS]] == | ||
| Строка 53: | Строка 52: | ||
: df = 4406 , a = 0,05, t* = 1.96 | : df = 4406 , a = 0,05, t* = 1.96 | ||
: r2 = 0,6471 | : r2 = 0,6471 | ||
=== Встраиваемый шаблон === | |||
<nowiki>{{Шаблон:CODAP Results Glossary}}</nowiki> | |||
{{Шаблон:CODAP Results Glossary}} | |||
[[Category:Social_statistic_research]] | |||
Текущая версия от 11:59, 14 января 2026
| Описание | Как провести регрессионный анализ зависимости между двумя переменными. Мы используем CODAP |
|---|---|
| Область знаний | Статистика, Моделирование |
| Область использования (ISTE) | |
| Возрастная категория | 16
|
| Поясняющее видео | |
| Близкие рецепту понятия | МНК, Регрессия, Коэффициент корреляции |
| Среды и средства для приготовления рецепта: | CORGIS, CODAP, RAWGraphs, StatKey |
Датасет CORGIS
| Description | |
|---|---|
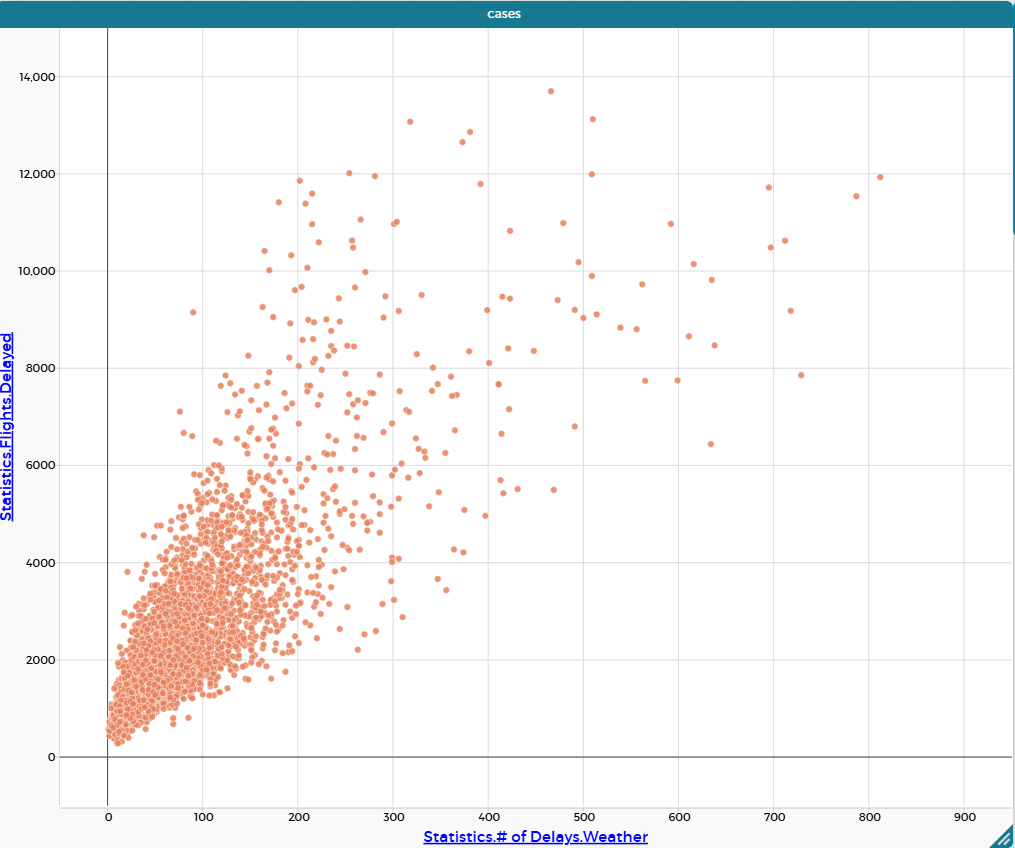
| Диаграмма рассеяния | Диаграмма рассеяния (scatter plot) — графический метод визуализации связи между двумя количественными переменными, где каждое наблюдение представлено точкой на координатной плоскости. |
Метод наименьших квадратов
| Description | |
|---|---|
| Метод наименьших квадратов | Метод наименьших квадратов (МНК) (англ. Least Squares Method, Ordinary Least Squares, OLS) — это математический метод оценки параметров статистических моделей, основанный на принципе минимизации суммы квадратов отклонений между наблюдаемыми и предсказанными моделью значениями. |
Регрессионный анализ
| Description | |
|---|---|
| Регрессионный анализ | Регрессио́нный анализ — набор статистических методов исследования влияния одной или нескольких независимых переменных на зависимую переменную. Независимые переменные иначе называют регрессорами или предикторами, а зависимые переменные — критериальными или регрессантами. Терминология зависимых и независимых переменных отражает лишь математическую зависимость переменных, а не причинно-следственные отношения. Наиболее распространённый вид регрессионного анализа — линейная регрессия, когда находят линейную функцию, которая, согласно определённым математическим критериям, наиболее соответствует данным. Например, в методе наименьших квадратов вычисляется прямая (или гиперплоскость), сумма квадратов между которой и данными минимальна. |
В CODAP регрессионный анализ проводится при помощи расширения testimate
Подробный анализ полученного результата:
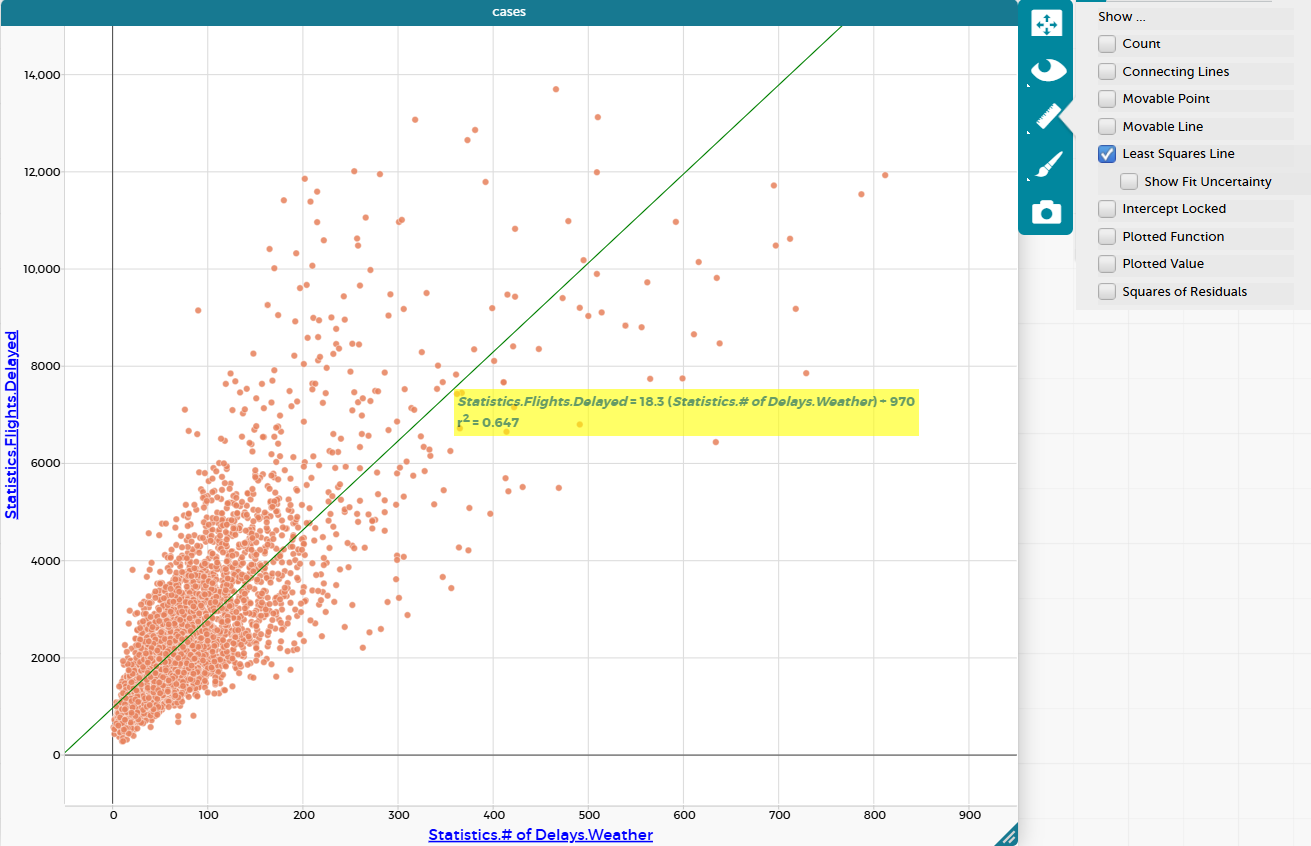
Регрессионный анализ с использованием метода наименьших квадратов
- LSRL: Statistics.Flights.Delayed = 18,31 (Statistics.# of Delays.Weather) - NaN
- Для каждого дополнительного случая задержки из-за погоды ожидается увеличение количества задержанных рейсов на 18,31 рейса в среднем.
- N = 4408 — количество наблюдений (рейсов) в вашей выборке. Значительный размер выборки делает результаты более надежными.
- ρ (rho) = 0,8044 — это коэффициент корреляции Пирсона. Его значение может варьироваться от -1 до +1:
- 0,8044 указывает на очень сильную положительную корреляцию
- Коэффициент детерминации r2 = 0,6471 Интерпретация: Примерно 64,71% вариативности в количестве задержанных рейсов можно объяснить вариативностью в количестве задержек из-за погоды
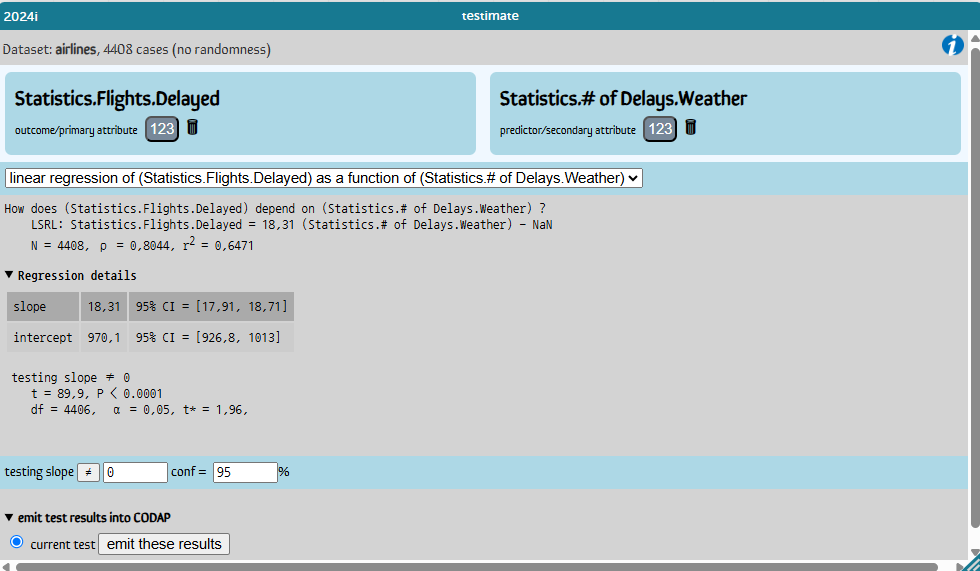
Детали анализа
- Regression details
- slope 18,31 95% CI = [17,91, 18,71] - Угловой коэффициент (наклон) = 18,31 — означает, что при увеличении количества задержек из-за погоды на одну единицу, количество задержанных рейсов увеличивается в среднем на 18,31 единицы
- intercept 970,1 95% CI = [926,8, 1013] Свободный член (пересечение с осью) = 970,1 — это прогнозируемое количество задержанных рейсов при нулевых погодных задержках.
- testing slope
- t = 89.9 P < 0.0001
- df = 4406 , a = 0,05, t* = 1.96
- r2 = 0,6471
Встраиваемый шаблон
{{Шаблон:CODAP Results Glossary}}
| Обозначение (CODAP) | Полное русское | Смысл / Интерпретация | Пример значения |
|---|---|---|---|
| N или n | Размер выборки (Sample size) | Количество наблюдений (объектов, студентов, случаев) в вашей выборке. Чем больше N, тем надежнее результаты. | N = 5000, N = 2332 |
| t | t-статистика или t-критерий Стьюдента | Стандартизованное число, которое показывает, на сколько стандартных ошибок среднее значение отличается от гипотетического значения. Вычисляется как: [math]\displaystyle{ t = \frac{\bar{x} - \mu_0}{SE} }[/math] | t = 167, t = 30,9 |
| P или p-value | p-значение (статистическая значимость) | Вероятность получить такое же или более экстремальное значение t-статистики при условии, что нулевая гипотеза верна. Если p < 0,05 (или p < 0,01), результат статистически значимый. | P < 0,0001 (очень значимый) |
| sample mean или [math]\displaystyle{ \bar{x} }[/math] | Выборочное среднее (Mean) | Среднее арифметическое всех значений в выборке. | 35,3; 11,1 |
| 95% CI или 95% ДИ | 95% доверительный интервал | Интервал, в котором с вероятностью 95% находится истинное среднее значение генеральной совокупности. Формула: [math]\displaystyle{ \bar{x} \pm t^* \times SE }[/math]. Если интервал узкий - оценка точная, если широкий - менее точная. | [34,85; 35,68], [10,4; 11,81] |
| s | Выборочное стандартное отклонение (Standard deviation) | Мера разброса данных вокруг среднего значения. Показывает, как сильно отдельные значения отличаются от среднего. Вычисляется как: [math]\displaystyle{ s = \sqrt{\frac{\sum(x_i - \bar{x})^2}{n-1}} }[/math] | s = 14,95; s = 17,34 |
| SE или SEM | Стандартная ошибка среднего (Standard Error of the Mean) | Мера точности выборочного среднего. Показывает, насколько выборочное среднее может отличаться от истинного среднего генеральной совокупности. Вычисляется как: [math]\displaystyle{ SE = \frac{s}{\sqrt{n}} }[/math]. Чем больше N, тем меньше SE. | SE = 0,2115; SE = 0,3591 |
| df | Степени свободы (Degrees of freedom) | Количество независимых наблюдений, которые могут меняться свободно при расчетах. Для одновыборочного t-теста: df = N - 1. Используется для определения критического значения t*. | df = 5000, df = 2330 |
| α (альфа) | Уровень значимости (Significance level) | Вероятность совершить ошибку первого рода (отвергнуть верную нулевую гипотезу). Стандартное значение: α = 0,05 (5%) или α = 0,01 (1%). Выбирается ДО анализа данных. | α = 0,05 |
| t* | Критическое значение t-распределения Стьюдента | t| > t*, результат статистически значимый. При больших N (n > 100) t* ≈ 1,96. | t* = 1,96 |