Обсуждение:Simple Economy
Исследование влияния частоты экономических транзакций на динамику неравенства в стохастической агентной модели. Выполнил студент группы ИНФА-241 Хлопков Вячеслав
Цель эксперимента
Изучить динамику распределения богатства в закрытой экономической системе, где агенты осуществляют случайные транзакции, и проанализировать механизмы возникновения экономического неравенства при изначально равных стартовых условиях.
Регрессионный анализ - первое приближение
Линейная регрессия максимального богатства как функции коэффициента Джини LSRL: max wealth = 1,695 × Gini - NaN N = 36, ρ = 0,9098, r² = 0,8277
Детали регрессии: Наклон: 1,695 (95% ДИ = [1,426, 1,965])
Пересечение: 21,07 (95% ДИ = [19,51, 22,62])
Проверка H₀: наклон = 0: t = 12,8, P < 0.0001
Степени свободы: 34, α = 0,05, t* = 2,03
Анализ временных рядов неравенства
Как модель собирает данные о динамике неравенства Модель фиксирует эволюцию распределения богатства во времени, позволяя анализировать:
Коэффициент Джини на каждом тике
Долю богатства у различных групп населения
Количество агентов в разных категориях богатства
Процентильные значения распределения
Эксперимент с параметром транзакционной активности
Цель эксперимента: исследовать, как вероятность участия в транзакциях влияет на динамику неравенства в системе. В ходе эксперимента варьировался параметр transaction-probability — вероятность того, что агент совершит транзакцию на каждом шаге.
Параметры эксперимента:
Количество агентов: 500
Начальное богатство: 100 у каждого
Количество шагов: 1000
Исследуемый параметр: вероятность транзакции p = 0.1, 0.3, 0.5, 0.7, 0.9, 1.0
Фиксированные параметры: величина транзакции = 1, начальное равенство (Gini = 0)
Полученные результаты
Малые значения вероятности транзакций (p = 0.1–0.3):

х- номер тика(шага) у- коэффициент Джини
- график сделан в аналоге desmos
https://docs.google.com/spreadsheets/d/1HlFjmxeL8ly2SknJz01EF3zhijyGT6jJgkUY9TVKpLY/edit?usp=sharing
Наблюдаемые явления:
Медленный рост неравенства
Коэффициент Джини достигает умеренных значений (0.3–0.5)
Распределение богатства сохраняет относительно нормальную форму
Меньшее количество агентов достигает нулевого богатства
Система демонстрирует высокую стабильность
Интерпретация: При низкой транзакционной активности система близка к равновесному состоянию. Случайные флуктуации компенсируются редкими взаимодействиями, что предотвращает быстрое накопление неравенства.
Оптимальное значение вероятности (p = 0.5):
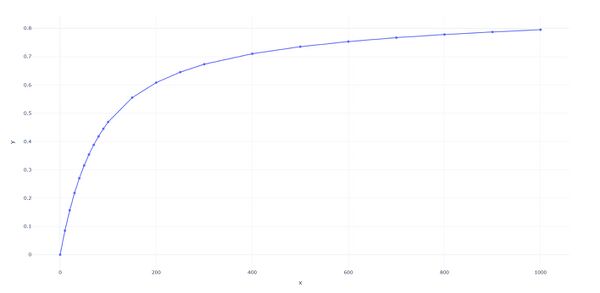
х- номер тика(шага) у- коэффициент Джини
- график сделан в аналоге desmos
https://docs.google.com/spreadsheets/d/18hIwtvmrVIRU_GznhO_f0mY36gas-9maxjENRzfNz_Y/edit?usp=sharing
Наблюдаемые явления:
Наиболее сбалансированная динамика
Коэффициент Джини стабилизируется на уровне ~0.6–0.7
Формируется устойчивое логнормальное распределение
Появляется выраженный "средний класс"
Экстремальные значения богатства (очень бедные/очень богатые) составляют меньшинство
Интерпретация: При умеренной активности достигается оптимальный баланс между стохастичностью взаимодействий и возможностью системы к саморегуляции. Формируется социально устойчивая структура с доминированием среднего класса.
Высокие значения вероятности (p = 0.7–1.0):
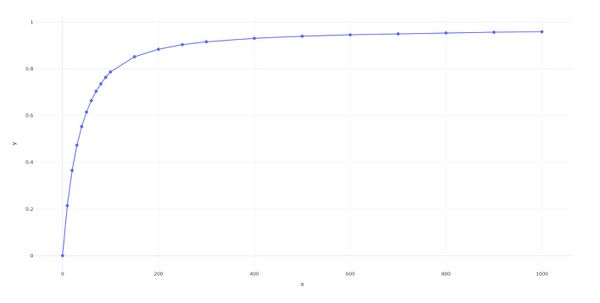
х- номер тика(шага) у- коэффициент Джини
- график сделан в аналоге desmos
https://docs.google.com/spreadsheets/d/1maN3kjUihHSGAcKErVacUhrTHVpB3aOfcDQMBHs27uw/edit?usp=sharing
Наблюдаемые явления:
Быстрый экспоненциальный рост неравенства
Коэффициент Джини достигает значений 0.8–0.9
Формируется крайне асимметричное распределение с "длинным хвостом"
Большинство агентов (60-70%) концентрируются вблизи нулевого богатства
Небольшая группа агентов (1-2%) аккумулирует 30-40% всего богатства
Появляются выраженные "олигархи" с богатством > 500
Интерпретация: Высокая транзакционная активность ускоряет процесс концентрации богатства. Система быстро достигает состояния, когда небольшое количество агентов доминирует в экономике, а большинство исключается из активных экономических взаимодействий.
Статистический анализ результатов
Фазовые переходы в системе: Фаза низкой активности (p < 0.3): Квазиравновесное состояние
Фаза умеренной активности (0.3 < p < 0.6): Формирование социальных структур
Фаза высокой активности (p > 0.6): Быстрая поляризация и олигархизация
Ключевые выводы
Нелинейная зависимость: Влияние транзакционной активности на неравенство имеет нелинейный характер с точкой перегиба при p ≈ 0.5.
Оптимум активности: Существует оптимальный уровень экономической активности (p ≈ 0.5), при котором система демонстрирует наиболее устойчивое и сбалансированное развитие.
Эффект гипер-активности: Чрезмерная экономическая активность (p > 0.7) приводит к быстрой дестабилизации системы и экстремальному неравенству.
Транзакционный механизм неравенства: Даже в симметричных условиях высокая частота экономических взаимодействий сама по себе является драйвером неравенства.
Политическая импликация: Регулирование частоты и объема экономических транзакций может быть эффективным инструментом контроля над уровнем неравенства.
Изменение распределения богатства со временем в модели Simple Economy
Цель: Исследовать, как случайный обмен ресурсами влияет на социальное неравенство.
В ходе исследования была использована агент-ориентированная модель Simple Economy, реализованная в среде NetLogo. Модель предназначена для изучения процессов распределения ресурсов в искусственном обществе, состоящем из автономных агентов, взаимодействующих по простым вероятностным правилам.
Начальные условия модели:
На этапе инициализации модели (команда setup) все агенты получали одинаковый объём начального богатства, что обеспечивало равенство стартовых условий и исключало влияние первоначального неравенства на результаты эксперимента. Пространственное распределение агентов и параметры их поведения задавались автоматически в соответствии с алгоритмом модели.
Процедура эксперимента:
После инициализации модель запускалась в режиме динамического развития (команда go). В каждом дискретном временном шаге (tick) происходили случайные взаимодействия между агентами, в рамках которых осуществлялся обмен единицей ресурса. Обмен носил стохастический характер и не зависел от социального статуса или текущего уровня богатства агентов.
В ходе эксперимента структура модели и правила взаимодействия не изменялись. Единственным варьируемым параметром являлось время моделирования, выраженное в количестве временных шагов (ticks). Наблюдение за состоянием системы осуществлялось на различных этапах её эволюции (100, 300 и 500 временных шагов).
Методы сбора данных:
Для анализа результатов использовались встроенные инструменты визуализации модели:
гистограмма распределения богатства между агентами (wealth distribution).
Данные фиксировались в дискретные моменты времени, что позволило проследить динамику изменения распределения ресурсов.
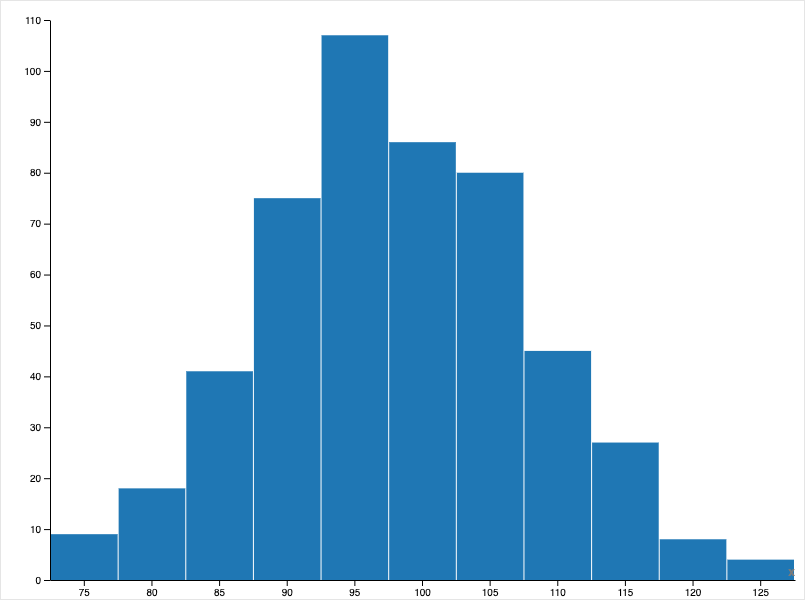
Результат после 100 временных шагов:
После 100 временных шагов в системе начинают проявляться первые признаки неравномерного распределения богатства. Хотя различия между агентами ещё относительно невелики, наблюдается отклонение от исходного равенства: часть агентов накапливает больше ресурсов, в то время как у других уровень богатства снижается. График распределения демонстрирует концентрацию агентов вблизи начальных значений с формированием начального «хвоста» в сторону более высоких уровней богатства. Таким образом, уже на раннем этапе моделирования фиксируется начало процесса экономического расслоения.
Результат после 300 временных шагов:
К 300 шагу неравенство становится выраженным и устойчивым. Распределение богатства приобретает асимметричный характер: значительно увеличивается доля агентов с низким уровнем ресурсов, одновременно формируется отчётливо различимая группа агентов с высоким уровнем богатства. Разрыв между суммарным богатством верхних 10 % и нижних 50 % возрастает, что свидетельствует об усилении концентрации ресурсов. По сравнению с 100 шагами наблюдается качественное изменение структуры системы — неравенство перестаёт быть случайным отклонением и приобретает системный характер.
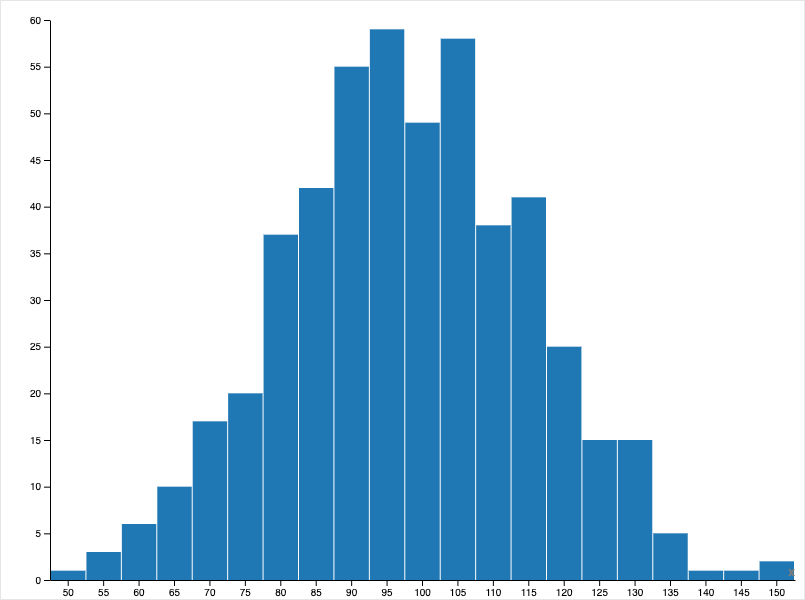
Результат после 500 временных шагов:
После 500 временных шагов распределение богатства стабилизируется в форме выраженного социально-экономического неравенства. Большинство агентов оказывается сосредоточено в зоне минимальных и низких значений богатства, тогда как ограниченное число агентов аккумулирует значительную часть ресурсов системы. Изменения по сравнению с 300 шагами носят преимущественно количественный характер: усиливается концентрация богатства у наиболее обеспеченной группы, а положение наименее обеспеченных агентов остаётся устойчиво неблагоприятным. Это указывает на формирование устойчивого неравновесного состояния, сохраняющегося при дальнейшем развитии модели.
Эксперимент показал, что в модели Simple Economy экономическое неравенство формируется даже при равных начальных условиях распределения ресурсов: в ходе моделирования большинство агентов концентрируется в зоне низких и средних значений богатства, тогда как небольшая группа аккумулирует существенно больший объём ресурсов; при этом число агентов последовательно уменьшается с ростом уровня богатства, что указывает на асимметричное распределение, возникающее за счёт внутренней динамики системы и случайного характера агентных взаимодействий, без введения дополнительных внешних факторов.