Кривая Лоренца: различия между версиями
Patarakin (обсуждение | вклад) |
Patarakin (обсуждение | вклад) |
||
| Строка 1: | Строка 1: | ||
{{Понятие | {{Понятие | ||
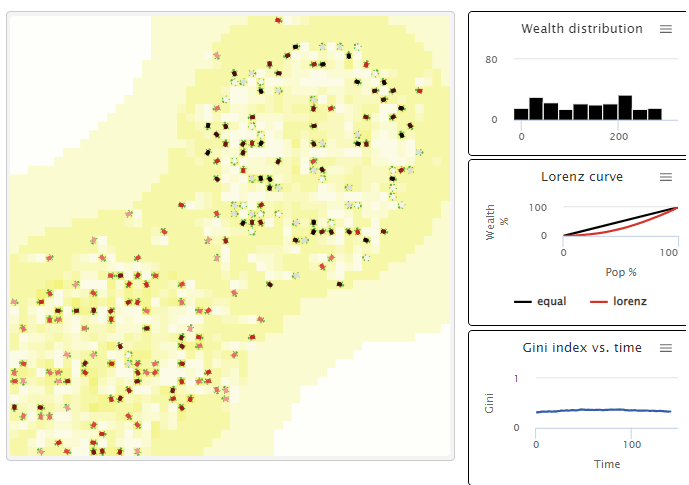
|Description=Кривая Лоренца (англ. Lorenz curve) — графическое изображение функции распределения, предложенная американским экономистом Максом Отто Лоренцем в 1905 году как показатель неравенства в доходах населения. Кривая Лоренца представляет функцию распределения, в которой аккумулируются доли численности и доходов населения. В прямоугольной системе координат кривая Лоренца является выпуклой вниз и проходит под диагональю единичного квадрата, расположенного в I координатной четверти. | |Description=Кривая Лоренца (англ. Lorenz curve) — графическое изображение функции распределения, предложенная американским экономистом Максом Отто Лоренцем в 1905 году как показатель неравенства в доходах населения. Кривая Лоренца представляет функцию распределения, в которой аккумулируются доли численности и доходов населения. В прямоугольной системе координат кривая Лоренца является выпуклой вниз и проходит под диагональю единичного квадрата, расположенного в I координатной четверти. | ||
|Field_of_knowledge=Экономика, Статистика | |||
|Inventor=Лоренц | |Inventor=Лоренц | ||
|similar_concepts=Коэффициент Джини | |similar_concepts=Коэффициент Джини | ||
Текущая версия на 18:06, 22 мая 2024
| Описание | Кривая Лоренца (англ. Lorenz curve) — графическое изображение функции распределения, предложенная американским экономистом Максом Отто Лоренцем в 1905 году как показатель неравенства в доходах населения. Кривая Лоренца представляет функцию распределения, в которой аккумулируются доли численности и доходов населения. В прямоугольной системе координат кривая Лоренца является выпуклой вниз и проходит под диагональю единичного квадрата, расположенного в I координатной четверти. |
|---|---|
| Область знаний | Экономика, Статистика |
| Авторы | Лоренц |
| Поясняющее видео | |
| Близкие понятия | Коэффициент Джини |
| Среды и средства для освоения понятия | Sugarscape model |
Формула
Формально, если [math]\displaystyle{ p=F(x) }[/math] — это доля населения с подушевым доходом не более [math]\displaystyle{ x }[/math], т.е. функция распределения для дохода, то средний доход на душу населения [math]\displaystyle{ \mu }[/math] можно вычислить по формуле
- [math]\displaystyle{ {\mu} = {\int_{0}^{\infty} x\,dF} = {\int_{0}^{\infty} x\,f(x)\,dx} , }[/math]
где [math]\displaystyle{ f(x) }[/math] есть плотность распределения для [math]\displaystyle{ F(x) }[/math], если она существует. Если [math]\displaystyle{ 0 \lt {\mu} \lt +\infty, }[/math] то функция Лоренца определяется формулой
- [math]\displaystyle{ L(p) = L(F(x)) = \frac{\int_{0}^{x} t\,f(t)\,dt}{\int_{0}^{\infty} t\,f(t)\,dt} = \frac{\int_{0}^{x} t\,f(t)\,dt}{\mu} }[/math]
(при [math]\displaystyle{ {\mu} = 0 }[/math] или [math]\displaystyle{ {\mu} = +\infty }[/math] функция Лоренца не определена). График функции Лоренца называется кривой Лоренца. Если существует обратная функция [math]\displaystyle{ x = F^{-1}(p) }[/math], то
- [math]\displaystyle{ L(p) = \frac{\int_{0}^{p} F^{-1}(p)\,dp}{\int_{0}^{1} F^{-1}(p)\,dp}. }[/math]
Пример. Если [math]\displaystyle{ F(x)=x^n }[/math] при [math]\displaystyle{ 0\le x\le 1 }[/math] и [math]\displaystyle{ F(x)=1 }[/math] при [math]\displaystyle{ x\ge 1 }[/math], то [math]\displaystyle{ L(p)=p^{1+\frac1{n}} }[/math]. При [math]\displaystyle{ n\to+\infty }[/math] функция распределения стремится к функции скачка в точке 1, отвечающей равномерному распределению дохода, а [math]\displaystyle{ L(p)\to p }[/math], то есть кривая Лоренца стремится к кривой равенства.
Присутствие точки [math]\displaystyle{ (p,L(p)) }[/math] на кривой Лоренца означает, что доля [math]\displaystyle{ p }[/math] самых бедных жителей совокупно обладает долей [math]\displaystyle{ L(p) }[/math] общего дохода. Например, на приведенном ниже рисунке видно, что на примерно 3/4 самых бедных жителей приходится примерно половина всех доходов.
см. Sugarscape model