Big O notation: различия между версиями
Patarakin (обсуждение | вклад) |
Patarakin (обсуждение | вклад) |
||
| Строка 3: | Строка 3: | ||
|Field_of_knowledge=Информатика | |Field_of_knowledge=Информатика | ||
|Inventor=Бахман | |Inventor=Бахман | ||
|Clarifying_video=https://www.youtube.com/watch?v=cXCuXNwzdfY | |||
|similar_concepts=Временная сложность алгоритма | |similar_concepts=Временная сложность алгоритма | ||
|Environment=Snap!, JavaScript, Python | |Environment=Snap!, JavaScript, Python | ||
}} | }} | ||
Big O нотация нужна для описания сложности алгоритмов. | Big O нотация нужна для описания сложности алгоритмов. | ||
Обозначение «„O“ большое» введено немецким математиком Паулем Бахманом во втором томе его книги «Analytische Zahlentheorie» (Аналитическая теория чисел), вышедшем в 1894 году. | Обозначение «„O“ большое» введено немецким математиком Паулем Бахманом во втором томе его книги «Analytische Zahlentheorie» (Аналитическая теория чисел), вышедшем в 1894 году. | ||
Текущая версия на 21:10, 4 марта 2023
| Описание | «O» большое — математические обозначения для сравнения асимптотического поведения (асимптотики) функций. Используются в различных разделах математики, но активнее всего — в математическом анализе, теории чисел и комбинаторике, а также в информатике и теории алгоритмов. |
|---|---|
| Область знаний | Информатика |
| Авторы | Бахман |
| Поясняющее видео | https://www.youtube.com/watch?v=cXCuXNwzdfY |
| Близкие понятия | Временная сложность алгоритма |
| Среды и средства для освоения понятия | Snap!, JavaScript, Python |
Big O нотация нужна для описания сложности алгоритмов. Обозначение «„O“ большое» введено немецким математиком Паулем Бахманом во втором томе его книги «Analytische Zahlentheorie» (Аналитическая теория чисел), вышедшем в 1894 году. Чтобы понять, что такое О большое, мы можем взглянуть на типичный пример O (n²), который обычно произносится как «Большой O в квадрате»
Определения
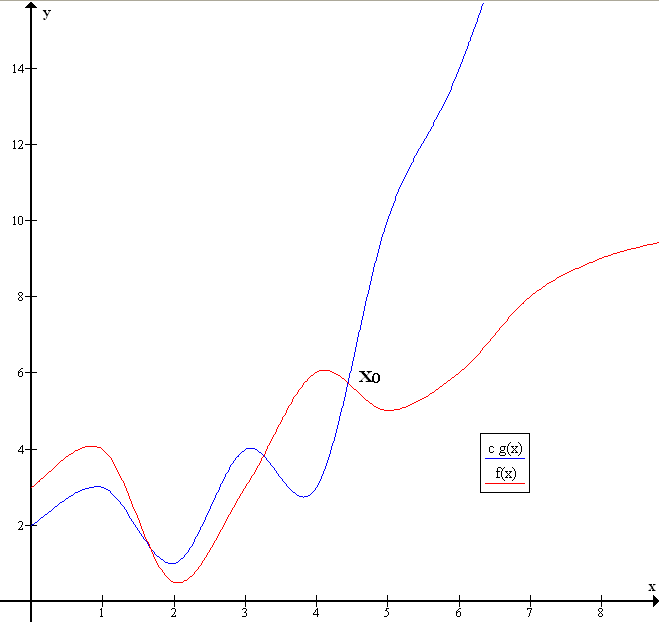
Пусть [math]\displaystyle{ f(x) }[/math] и [math]\displaystyle{ g(x) }[/math] — две функции, определенные в некоторой проколотой окрестности точки [math]\displaystyle{ x_0 }[/math], причем в этой окрестности [math]\displaystyle{ g }[/math] не обращается в ноль. Говорят, что:
- [math]\displaystyle{ f }[/math] является «O» большим от [math]\displaystyle{ g }[/math] при [math]\displaystyle{ x\to x_0 }[/math], если существует такая константа [math]\displaystyle{ C\gt 0 }[/math], что для всех [math]\displaystyle{ x }[/math] из некоторой окрестности точки [math]\displaystyle{ x_0 }[/math] имеет место неравенство
- [math]\displaystyle{ |f(x)| \leqslant C |g(x)| }[/math];
- [math]\displaystyle{ f }[/math] является «о» малым от [math]\displaystyle{ g }[/math] при [math]\displaystyle{ x\to x_0 }[/math], если для любого [math]\displaystyle{ \varepsilon\gt 0 }[/math] найдется такая проколотая окрестность [math]\displaystyle{ U_{x_0}' }[/math] точки [math]\displaystyle{ x_0 }[/math], что для всех [math]\displaystyle{ x\in U_{x_0}' }[/math] имеет место неравенство
- [math]\displaystyle{ |f(x)| \lt \varepsilon |g(x)|. }[/math]
Иначе говоря, в первом случае отношение [math]\displaystyle{ \frac{|f|}{|g|} \leqslant C }[/math] в окрестности точки [math]\displaystyle{ x_0 }[/math] (то есть ограничено сверху), а во втором оно стремится к нулю при [math]\displaystyle{ x\to x_0 }[/math].