Коэффициент Джини

Описание	Коэффициент Джини — статистический показатель степени расслоения общества данной страны или региона по какому-либо изучаемому признаку. Используется для оценки экономического неравенства. Коэффициент Джини может варьироваться между 0 и 1. Чем больше его значение отклоняется от нуля и приближается к единице, тем в большей степени доходы сконцентрированы в руках отдельных групп населения.
Область знаний	Экономика
Авторы	Джини
Поясняющее видео
Близкие понятия	Кривая Лоренца
Среды и средства для освоения понятия

Эта статистическая модель была предложена и разработана итальянским статистиком и демографом Коррадо Джини и опубликована в 1912 году в его труде «Вариативность и изменчивость признака» («Изменчивость и непостоянство»).

Рассчитать коэффициент можно как отношение площади фигуры, образованной кривой Лоренца и прямой равенства, к площади треугольника, образованного прямой равенства и осями. Иначе говоря, следует найти площадь первой фигуры и поделить её на площадь второй. В случае полного равенства коэффициент будет равен 0; в случае полного неравенства он будет равен 1.

Коэффициент Джини можно рассчитать по формуле Брауна:

[math]\displaystyle{ G=\left\vert 1-\sum_{k=2}^n (X_k - X_{k-1})(Y_k + Y_{k-1}) \right\vert }[/math],

или по формуле Джини:

[math]\displaystyle{ G=\frac {\sum\limits_{i=1}^n \sum\limits_{j=1}^n\left\vert y_i - y_j \right\vert }{ 2 n^2 \bar{y}} }[/math],

где [math]\displaystyle{ G }[/math] — коэффициент Джини, [math]\displaystyle{ X_k }[/math] — кумулированная доля населения (население предварительно ранжировано по возрастанию доходов), [math]\displaystyle{ Y_k }[/math] — доля дохода, которую в совокупности получает [math]\displaystyle{ X_k }[/math], [math]\displaystyle{ n }[/math] — число домохозяйств, [math]\displaystyle{ y_k }[/math] — доля дохода домохозяйства в общем доходе, [math]\displaystyle{ \bar{y} }[/math] — среднее арифметическое долей доходов домохозяйств

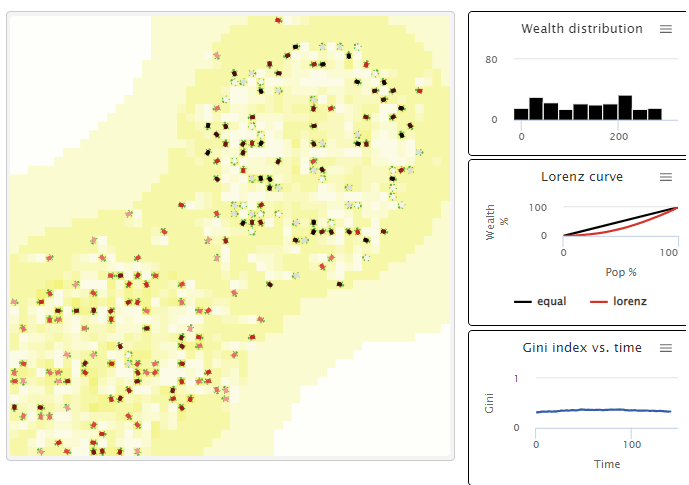• см. Sugarscape model
• Wealth Distribution - Коэффициент Джини = 0.56 означает значительное неравенство.

Рассчитайте коэффициент Джини для заданного распределения (используя данные симуляции Wealth Distribution)