Смертность: различия между версиями
Patarakin (обсуждение | вклад) |
Patarakin (обсуждение | вклад) |
||
| (не показано 7 промежуточных версий этого же участника) | |||
| Строка 2: | Строка 2: | ||
|Description=Сме́ртность — свойство живых организмов быть подверженными смерти. | |Description=Сме́ртность — свойство живых организмов быть подверженными смерти. | ||
|Field_of_knowledge=Биология | |Field_of_knowledge=Биология | ||
|Environment=StarLogo Nova, | |similar_concepts=Рождение, Размножение | ||
|Environment=StarLogo Nova, NetLogo | |||
}} | }} | ||
Закон смертности Гомпертца — Мейкхама (иногда просто Закон Гомпертца, Распределение Гомпертца) — статистическое распределение, которое описывает смертность человека и большинства многоплодных животных. Согласно закону Гомпертца — Мейкхама, смертность является суммой независимого от возраста компонента (члена Мейкхама) и компонента, зависимого от возраста (функция Гомпертца), который экспоненциально возрастает с возрастом и описывает старение | Закон смертности Гомпертца — Мейкхама (иногда просто Закон Гомпертца, Распределение Гомпертца) — статистическое распределение, которое описывает смертность человека и большинства многоплодных животных. Согласно закону Гомпертца — Мейкхама, смертность является суммой независимого от возраста компонента (члена Мейкхама) и компонента, зависимого от возраста (функция Гомпертца), который [[экспонента|экспоненциально]] возрастает с возрастом и описывает старение [[организм]]а. В защищённых средах, где внешние причины смерти отсутствуют (в лабораторных условиях, в зоопарках или для людей в развитых странах) независимый от возраста компонент часто становится малым, и формула упрощается до функции Гомпертца. | ||
Согласно закону Гомпертца — Мейкхама, вероятность смерти за фиксированный короткий промежуток времени после достижения возраста '''x''' составляет: | Согласно закону Гомпертца — Мейкхама, вероятность смерти за фиксированный короткий промежуток времени после достижения возраста '''x''' составляет: | ||
| Строка 22: | Строка 23: | ||
set alpha (0.085 * 0.5 / (exp(0.085 * life-expectancy) - 1)) | set alpha (0.085 * 0.5 / (exp(0.085 * life-expectancy) - 1)) | ||
ask turtles [ | ask turtles [ | ||
if random 1000 < (alpha * exp(0.085 * age)) * 1000 | |||
[ | |||
if random 1000 < (alpha * exp(0.085 * age)) * 1000 [ | |||
set ndeaths ndeaths + 1 | set ndeaths ndeaths + 1 | ||
die | die | ||
] | |||
] | |||
ifelse count turtles != 0 | |||
[set crude-death (ndeaths / count turtles) * 1000] | |||
[set crude-death 0] | |||
set deathrate-hist but-first deathrate-hist | |||
set deathrate-hist lput crude-death deathrate-hist | |||
set death-moving-avg mean deathrate-hist | |||
end | |||
</syntaxhighlight> | </syntaxhighlight> | ||
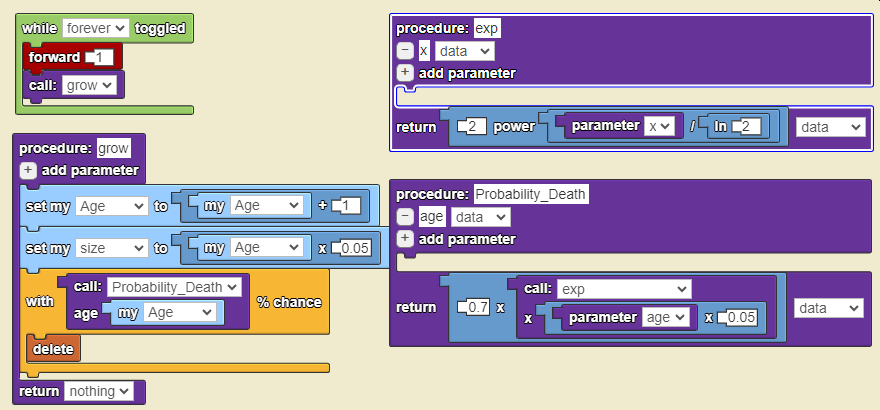
== StarLogo Nova == | == StarLogo Nova == | ||
[[Файл:Sl probability death.png]] | |||
* https://www.slnova.org/patarakin/projects/919658/ | |||
{{#widget:iframe | |||
|url=https://www.slnova.org/patarakin/projects/919658/ | |||
|width=800 | |||
|height=800 | |||
}} | |||
Текущая версия на 07:41, 4 мая 2024
| Описание | Сме́ртность — свойство живых организмов быть подверженными смерти. |
|---|---|
| Область знаний | Биология |
| Авторы | |
| Поясняющее видео | |
| Близкие понятия | Рождение, Размножение |
| Среды и средства для освоения понятия | StarLogo Nova, NetLogo |
Закон смертности Гомпертца — Мейкхама (иногда просто Закон Гомпертца, Распределение Гомпертца) — статистическое распределение, которое описывает смертность человека и большинства многоплодных животных. Согласно закону Гомпертца — Мейкхама, смертность является суммой независимого от возраста компонента (члена Мейкхама) и компонента, зависимого от возраста (функция Гомпертца), который экспоненциально возрастает с возрастом и описывает старение организма. В защищённых средах, где внешние причины смерти отсутствуют (в лабораторных условиях, в зоопарках или для людей в развитых странах) независимый от возраста компонент часто становится малым, и формула упрощается до функции Гомпертца.
Согласно закону Гомпертца — Мейкхама, вероятность смерти за фиксированный короткий промежуток времени после достижения возраста x составляет:
- [math]\displaystyle{ p=a+b\exp(cx) }[/math],
где x — возраст, а p — относительная вероятность смерти за определённый промежуток времени, a, b и c — коэффициенты.
NetLogo
to check-death
if ticks = 0 [set deathrate-hist [0 0 0 0 0 0 0 0 0 0]]
set alpha (0.085 * 0.5 / (exp(0.085 * life-expectancy) - 1))
ask turtles [
if random 1000 < (alpha * exp(0.085 * age)) * 1000
[
set ndeaths ndeaths + 1
die
]
]
ifelse count turtles != 0
[set crude-death (ndeaths / count turtles) * 1000]
[set crude-death 0]
set deathrate-hist but-first deathrate-hist
set deathrate-hist lput crude-death deathrate-hist
set death-moving-avg mean deathrate-hist
end
StarLogo Nova