Исследование зависимости числа переездов агентов от установленного порога толерантности на базе модели Segregation

Description

Segregation (model)

Модель сегрегации Модель сегрегации Шеллинга – это агент-ориентированная модель, которая иллюстрирует, как индивидуальные тенденции в отношении соседей могут привести к сегрегации. Модель особенно полезна для изучения жилищной сегрегации этнических групп, где агенты представляют домовладельцев, которые переселяются в город. В модели каждый агент принадлежит к одной из двух групп и стремится жить в районе, где доля "друзей" достаточно высока: выше определенного порогового значения F. В зависимости от F, для групп равного размера, модель проживания по Шеллингу сходится либо к полной интеграции (случайное распределение), либо к сегрегации. Принципы: Минимальная толерантность к различиям: Люди склонны предпочитать окружение, где большинство соседей принадлежат к той же группе, что и они сами. Однако они могут терпеть некоторую долю соседей другой группы. Пороговая толерантность: Существует пороговый уровень доли соседей другой группы, выше которого человек начинает чувствовать себя некомфортно и стремится переехать в район с большей однородностью. Переезд при превышении порога: Если доля соседей другой группы превышает установленный порог, человек решает переехать. Этот переезд приводит к тому, что районы становятся всё более сегрегированными.

Эксперимент: зависимость числа переездов от установленного порога толерантности

Запуск модели с базовыми настройками

Изначально агенты расселены хаотично, но с ростом числа переселений, наблюдается формирование нескольких больших районов. Возникает вопрос - как с изменением уровня толерантности будет изменяться время, за которое будут сформированы районы из которых никто не захочет переезжать?

Гипотеза

H0: При снижении уровня толерантности (увеличении значения %-similar-wanted), количество переездов (время за которое система достигает стабильного состояния) будет увеличиваться. При этом я предполагаю, что зависимость будет линейной. H1: Какая либо зависимость отсутствует.

Эксперимент

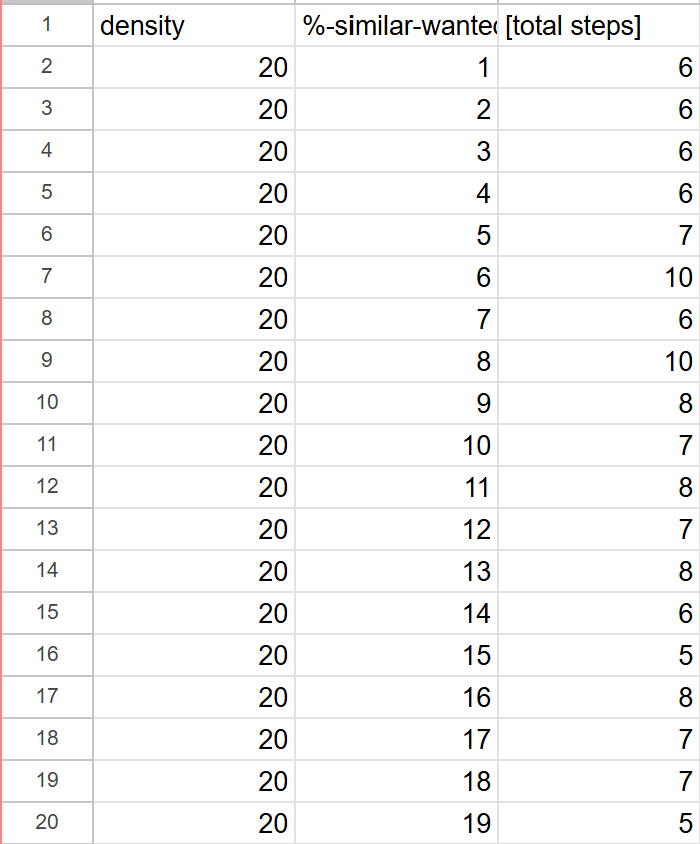
Для проведения эксперимента NetLogo был установлен локально. При помощи пространства поведения был подготовлен датасет. При сборе данных были вставлены следующие значения:

Плотность расселения: ["density" 10 20 30 40 50 60 70 80 90]

Порог толерантности: ["%-similar-wanted" 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100]

В результате был получен следующий датасет:

https://docs.google.com/spreadsheets/d/18oJPWpLzbByccITcyoA_w0GFR61MI-2DlRfxcplIH7s/edit?usp=sharing

Цель эксперимента:: установить тип зависимости (или ее отсутствие) времени достижения системой стабильного состояния от уровня толерантности.

На основе полученного датасета был сформирован график:

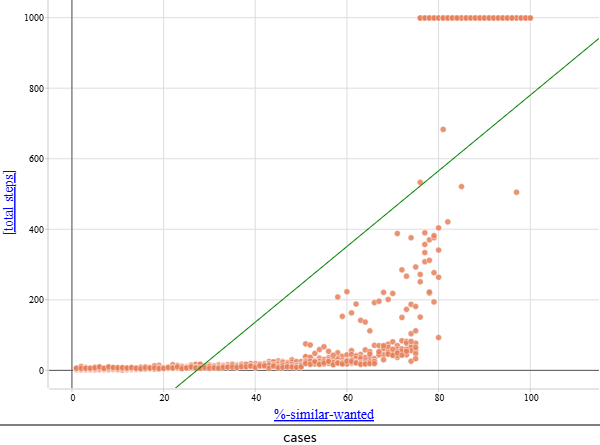
Регрессионный анализ:

How does ([total steps]) depend on (%-similar-wanted) ?

   LSRL: [total steps] = 10,73 (%-similar-wanted) - NaN 
   N = 800, ρ = 0,7664, r2 = 0,5874

Regression details slope 10,73 95% CI = [10,1, 11,35] intercept -292,5 95% CI = [-328,9, -256,2]

testing slope ≠ 0 
   t = 33,7, P < 0.0001
   df = 798,  α = 0,05, t* = 1,96,

Наблюдения и замечания

1. Значения на уровне 1000 не превышают из-за вручную выставленных ограничений модели. Если количество total steps равно 1000, можно считать что стабильное состояние для такой системы является недостижимым.

2. Для любой плотности расселения большей или равной 20, в промежутке similar-wanted = 70-80 наступает момент, когда стабильность становится недостижимой либо мало.

3. Наблюдаемая зависимость больше походит на экспоненциальную, нежели на линейную.