Обсуждение:Minority Game: различия между версиями
Patarakin (обсуждение | вклад) →Анализ временных рядов: новая тема |
Нет описания правки |
||
| (не показана 1 промежуточная версия этого же участника) | |||
| Строка 18: | Строка 18: | ||
* Как мы можем использовать модель для сбора данных | * Как мы можем использовать модель для сбора данных | ||
== Эксперимент с памятью агентов == | |||
Целью эксперимента было исследовать, как длина памяти агентов влияет на коллективное поведение системы в модели Minority Game. | |||
В ходе эксперимента были зафиксированы все параметры модели, кроме длины памяти: | |||
* количество агентов: 101 (нечётное число); | |||
* число стратегий у агента: 2; | |||
* число шагов моделирования: 300; | |||
* исследуемый параметр: длина памяти m. | |||
Рассматривались следующие значения памяти: m = 1, 2, 3, 6, 9, 12. | |||
В качестве результата анализировался временной график числа агентов, выбравших одну из стратегий, где идеальное коллективное поведение соответствует колебаниям около значения N/2 ≈ 50. | |||
'''Полученные результаты:''' | |||
{{#widget:Google Spreadsheet | |||
|key=e/2PACX-1vTNJBre6r5gEMktVrumeqOAxqIKRWHixi2Q6YguO_wlBtDOfZ0c1Kxu7nwwIrx6-YB1WJE7T_dCaSwb/ | |||
|width=250 | |||
|height=300 | |||
}} | |||
Данные были экспортированы из Netlogo, сохранены в представленной выше Google-таблице, и с помощью ПО для визуализации данных RAWGraphs представлены в виде графиков Linar Chart. | |||
'''Малые значения памяти (m = 1–3):''' | |||
[[Файл:Memory_one.jpg|400px|центр]] | |||
[[Файл:Memory_two.jpg|400px|центр]] | |||
[[Файл:Memory_three.jpg|400px|центр]] | |||
* Наблюдаются резкие и хаотичные колебания | |||
* Амплитуда колебаний велика | |||
* Часто фиксируются экстремальные значения, значительно удалённые от 50 | |||
* Поведение близко к случайному, без устойчивой структуры | |||
Агенты используют слишком мало информации из прошлого и не способны к эффективному обучению и координации. | |||
'''Промежуточное значение памяти (m = 6):''' | |||
[[Файл:Memory_six.jpg|400px|центр]] | |||
* Колебания становятся заметно более сглаженными | |||
* Большинство значений лежит в диапазоне примерно 45–55 | |||
* Амплитуда минимальна по сравнению с другими случаями | |||
* Выбросы редки и неустойчивы | |||
* График демонстрирует ограниченный шум без выраженного хаоса | |||
При данном значении памяти достигается наиболее эффективное коллективное поведение. | |||
'''Большие значения памяти (m = 9 и m = 12):''' | |||
[[Файл:Memory_nine.jpg|400px|центр]] | |||
[[Файл:Memory_twelve.jpg|400px|центр]] | |||
* Амплитуда колебаний снова возрастает | |||
* Появляются резкие скачки и сильные экстремумы: значения существенно ниже 40 и значения выше 60 | |||
* Поведение становится более «рваным» и нерегулярным | |||
* Разница между максимальными и минимальными значениями заметно увеличивается | |||
'''Результат:''' | |||
Эксперимент показал, что увеличение интеллектуальных возможностей отдельных агентов не всегда улучшает работу системы в целом: после некоторого оптимального значения памяти коллективное поведение становится менее устойчивым. | |||
Текущая версия от 09:54, 26 декабря 2025
Регрессионный анализ - первое приближение
linear regression of (max score of turtles) as a function of (memory) How does (max score of turtles) depend on (memory) ? LSRL: max score of turtles = 1,695 (memory) - NaN N = 36, ρ = 0,9098, r2 = 0,8277 Regression details slope 1,695 95% CI = [1,426, 1,965] intercept 21,07 95% CI = [19,51, 22,62] testing slope ≠ 0 t = 12,8, P < 0.0001 df = 34, α = 0,05, t* = 2,03,
Анализ временных рядов
- Как мы можем использовать модель для сбора данных
Эксперимент с памятью агентов
Целью эксперимента было исследовать, как длина памяти агентов влияет на коллективное поведение системы в модели Minority Game. В ходе эксперимента были зафиксированы все параметры модели, кроме длины памяти:
- количество агентов: 101 (нечётное число);
- число стратегий у агента: 2;
- число шагов моделирования: 300;
- исследуемый параметр: длина памяти m.
Рассматривались следующие значения памяти: m = 1, 2, 3, 6, 9, 12. В качестве результата анализировался временной график числа агентов, выбравших одну из стратегий, где идеальное коллективное поведение соответствует колебаниям около значения N/2 ≈ 50.
Полученные результаты:
Данные были экспортированы из Netlogo, сохранены в представленной выше Google-таблице, и с помощью ПО для визуализации данных RAWGraphs представлены в виде графиков Linar Chart.
Малые значения памяти (m = 1–3):
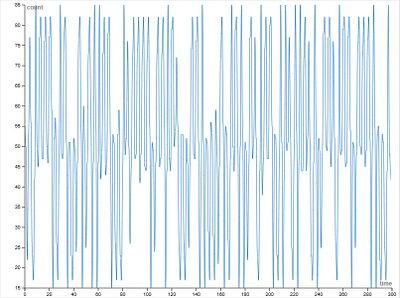
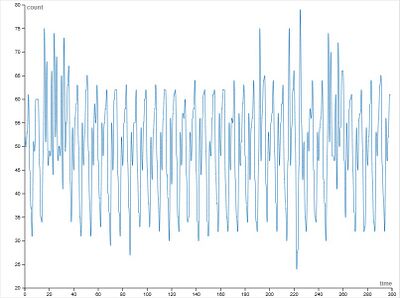
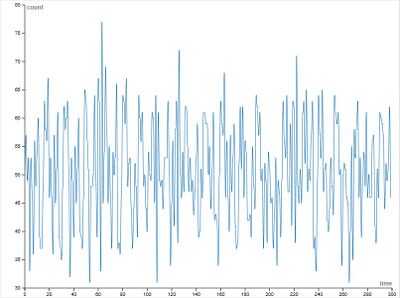
- Наблюдаются резкие и хаотичные колебания
- Амплитуда колебаний велика
- Часто фиксируются экстремальные значения, значительно удалённые от 50
- Поведение близко к случайному, без устойчивой структуры
Агенты используют слишком мало информации из прошлого и не способны к эффективному обучению и координации.
Промежуточное значение памяти (m = 6):
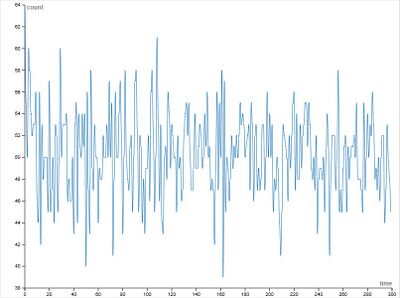
- Колебания становятся заметно более сглаженными
- Большинство значений лежит в диапазоне примерно 45–55
- Амплитуда минимальна по сравнению с другими случаями
- Выбросы редки и неустойчивы
- График демонстрирует ограниченный шум без выраженного хаоса
При данном значении памяти достигается наиболее эффективное коллективное поведение.
Большие значения памяти (m = 9 и m = 12):
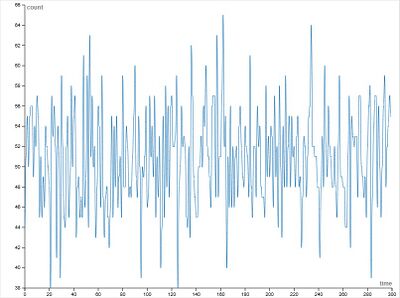
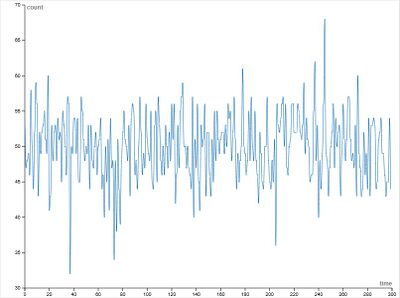
- Амплитуда колебаний снова возрастает
- Появляются резкие скачки и сильные экстремумы: значения существенно ниже 40 и значения выше 60
- Поведение становится более «рваным» и нерегулярным
- Разница между максимальными и минимальными значениями заметно увеличивается
Результат: Эксперимент показал, что увеличение интеллектуальных возможностей отдельных агентов не всегда улучшает работу системы в целом: после некоторого оптимального значения памяти коллективное поведение становится менее устойчивым.
