Исследование зависимости времени достижения стабильной сегрегации от порога толерантности на базе модели Segregation: различия между версиями
Новая страница: «{{#ask: Segregation (model)| ?Description }} == Эксперимент: зависимость числа переездов от установленного порога толерантности == === Запуск модели с базовыми настройками === Изначально агенты расселены хаотично, но с ростом числа переселений, наблюдается формирование не...» |
|||
| (не показана 1 промежуточная версия 1 участника) | |||
| Строка 22: | Строка 22: | ||
В результате был получен следующий датасет: | В результате был получен следующий датасет: | ||
{{#widget:Google Spreadsheet | |||
|key=e/2PACX-1vS-IfJSluYJN_R3NYqFOubcTi5rs3lPK8MCu_Gfmj7CFi63_zAQcusmcnk8E-JQpOEQEQtKQ-U967fW/ | |||
|width=800 | |||
|height=400 | |||
}} | |||
| Строка 48: | Строка 52: | ||
t = 33,7, P < 0.0001 | t = 33,7, P < 0.0001 | ||
df = 798, α = 0,05, t* = 1,96, | df = 798, α = 0,05, t* = 1,96, | ||
{{Шаблон:CODAP Results Glossary}} | |||
=== Наблюдения и замечания === | === Наблюдения и замечания === | ||
Текущая версия от 09:32, 27 декабря 2025
| Description | |
|---|---|
| Segregation (model) | Модель сегрегации
Принципы:
|
Эксперимент: зависимость числа переездов от установленного порога толерантности
Запуск модели с базовыми настройками
Изначально агенты расселены хаотично, но с ростом числа переселений, наблюдается формирование нескольких больших районов. Возникает вопрос - как с изменением уровня толерантности будет изменяться время, за которое будут сформированы районы из которых никто не захочет переезжать?
Гипотеза
H0: При снижении уровня толерантности (увеличении значения %-similar-wanted), количество переездов (время за которое система достигает стабильного состояния) будет увеличиваться. При этом я предполагаю, что зависимость будет линейной.
H1: Какая либо зависимость отсутствует.
Эксперимент
Для проведения эксперимента NetLogo был установлен локально. При помощи пространства поведения был подготовлен датасет. При сборе данных были вставлены следующие значения:
Плотность расселения: ["density" 10 20 30 40 50 60 70 80 90]
Порог толерантности: ["%-similar-wanted" 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100]
В результате был получен следующий датасет:
https://docs.google.com/spreadsheets/d/18oJPWpLzbByccITcyoA_w0GFR61MI-2DlRfxcplIH7s/edit?usp=sharing
Цель эксперимента:: установить тип зависимости (или ее отсутствие) времени достижения системой стабильного состояния от уровня толерантности.
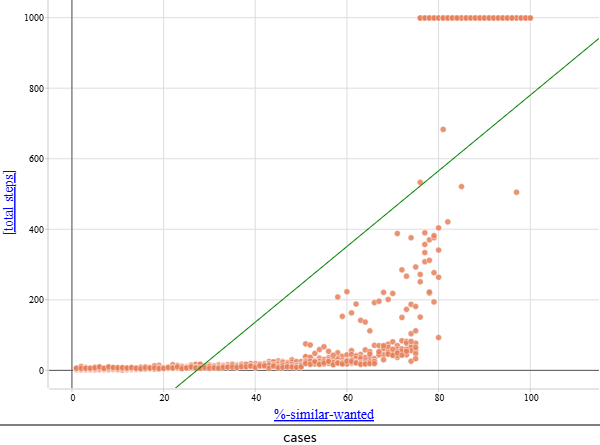
На основе полученного датасета был сформирован график:
Регрессионный анализ:
How does ([total steps]) depend on (%-similar-wanted) ?
LSRL: [total steps] = 10,73 (%-similar-wanted) - NaN N = 800, ρ = 0,7664, r2 = 0,5874
Regression details slope 10,73 95% CI = [10,1, 11,35] intercept -292,5 95% CI = [-328,9, -256,2]
testing slope ≠ 0 t = 33,7, P < 0.0001 df = 798, α = 0,05, t* = 1,96,
| Обозначение (CODAP) | Полное русское | Смысл / Интерпретация | Пример значения |
|---|---|---|---|
| N или n | Размер выборки (Sample size) | Количество наблюдений (объектов, студентов, случаев) в вашей выборке. Чем больше N, тем надежнее результаты. | N = 5000, N = 2332 |
| t | t-статистика или t-критерий Стьюдента | Стандартизованное число, которое показывает, на сколько стандартных ошибок среднее значение отличается от гипотетического значения. Вычисляется как: [math]\displaystyle{ t = \frac{\bar{x} - \mu_0}{SE} }[/math] | t = 167, t = 30,9 |
| P или p-value | p-значение (статистическая значимость) | Вероятность получить такое же или более экстремальное значение t-статистики при условии, что нулевая гипотеза верна. Если p < 0,05 (или p < 0,01), результат статистически значимый. | P < 0,0001 (очень значимый) |
| sample mean или [math]\displaystyle{ \bar{x} }[/math] | Выборочное среднее (Mean) | Среднее арифметическое всех значений в выборке. . | 35,3; 11,1 |
| 95% CI или 95% ДИ | 95% доверительный интервал | Интервал, в котором с вероятностью 95% находится истинное среднее значение генеральной совокупности. Формула: [math]\displaystyle{ \bar{x} \pm t^* \times SE }[/math]. Если интервал узкий - оценка точная, если широкий - менее точная. | [34,85; 35,68], [10,4; 11,81] |
| s | Выборочное стандартное отклонение (Standard deviation) | Мера разброса данных вокруг среднего значения. Показывает, как сильно отдельные значения отличаются от среднего. Вычисляется как: [math]\displaystyle{ s = \sqrt{\frac{\sum(x_i - \bar{x})^2}{n-1}} }[/math] | s = 14,95; s = 17,34 |
| SE или SEM | Стандартная ошибка среднего (Standard Error of the Mean) | Мера точности выборочного среднего. Показывает, насколько выборочное среднее может отличаться от истинного среднего генеральной совокупности. Вычисляется как: [math]\displaystyle{ SE = \frac{s}{\sqrt{n}} }[/math]. Чем больше N, тем меньше SE. | SE = 0,2115; SE = 0,3591 |
| df | Степени свободы (Degrees of freedom) | Количество независимых наблюдений, которые могут меняться свободно при расчетах. Для одновыборочного t-теста: df = N - 1. Используется для определения критического значения t*. | df = 5000, df = 2330 |
| α (альфа) | Уровень значимости (Significance level) | Вероятность совершить ошибку первого рода (отвергнуть верную нулевую гипотезу). Стандартное значение: α = 0,05 (5%) или α = 0,01 (1%). Выбирается ДО анализа данных. | α = 0,05 |
| t* | Критическое значение t-распределения Стьюдента | t| > t*, результат статистически значимый. При больших N (n > 100) t* ≈ 1,96. | t* = 1,96 |
Наблюдения и замечания
1. Значения равные 1000, не становятся больше, из-за вручную выставленных ограничений модели. Если количество total steps равно 1000, можно считать что стабильное состояние для такой системы является недостижимым.
2. Для любой плотности расселения большей или равной 20, в промежутке similar-wanted = 70-80 наступает момент, когда стабильность становится недостижимой, либо мало вероятной.
3. Наблюдаемая зависимость больше походит на экспоненциальную, нежели на линейную.
Выводы
По итогам исследования, можно сделать следующие выводы: изначальные гипотезы были ошибочны - как и предполагалось в нулевой теории, зависимость присутствует, однако она не линейная, а экспоненциальная.
Значение для экономики
Мое заключение базируется в основном на втором наблюдении. При высоком уровне требований к гомогенности окружения (70–80% и выше), даже при умеренной плотности населения (≥20%), система теряет способность достигать устойчивого равновесия. Это означает, что в реальных экономических системах — например, на рынке аренды или покупки жилья — чрезмерная «избирательность» участников (будь то по этническому, социальному или экономическому признаку) может привести к хронической нестабильности, постоянной миграции, росту транзакционных издержек и снижению общей эффективности распределения жилищных ресурсов.