Обсуждение:Random Basic Advanced
Эксперимент с моделью Random Basic Advanced
Цель эксперимента — исследовать, как параметры случайного выбора — размер пространства значений (sample-space) и количество агентов (num-messengers) — влияют на:
- форму распределения случайных значений;
- характер и устойчивость распределения средних значений;
- амплитуду колебаний и наличие экстремумов;
- степень «сглаживания» случайности при усреднении.
Для эксперимента были собраны данные с помощью Netlogo, они были экспортированы в CSV-таблицу, с помощью которой были созданы графики через веб-инструмент визуализации данных RAWGraphs в формате Bar Chart Эксперимент направлен на анализ того, насколько коллективное усреднение снижает хаотичность индивидуального случайного поведения.
Параметры модели
Изменяемые параметры:
- sample-space — диапазон возможных случайных значений;
- num-messengers — количество messengers в одной партии.
Наблюдаемые показатели:
- гистограмма All Values From Messengers — распределение всех случайных значений;
- гистограмма Mean Values of Batches of Messengers — распределение средних значений партий.
Проведённые прогоны:
Прогон 1 — малый диапазон, малое число messengers
- sample-space = 10
- num-messengers = 3
All Values From Messengers:
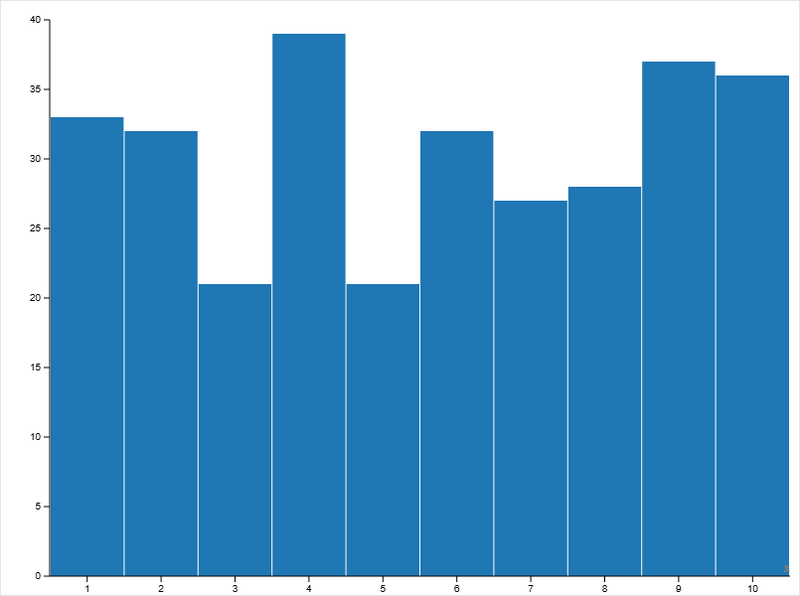
- значения распределены относительно равномерно;
- максимум частоты — в диапазоне 30–39;
- экстремальных выбросов нет.
Mean Values of Batches:
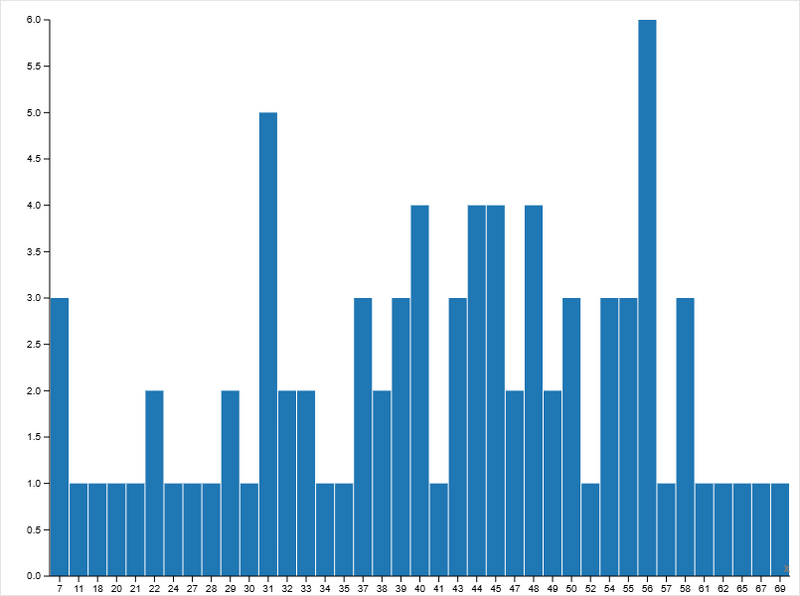
- средние значения распределены широко;
- заметны пики при средних значениях 4–6;
- разница между минимальным и максимальным средним значением велика.
Малое число messengers приводит к высокой чувствительности среднего значения к отдельным случайным выборам. Усреднение выражено слабо, средние значения нестабильны.
Прогон 2 — большой диапазон, малое число messengers
- sample-space = 80
- num-messengers = 3
All Values From Messengers:
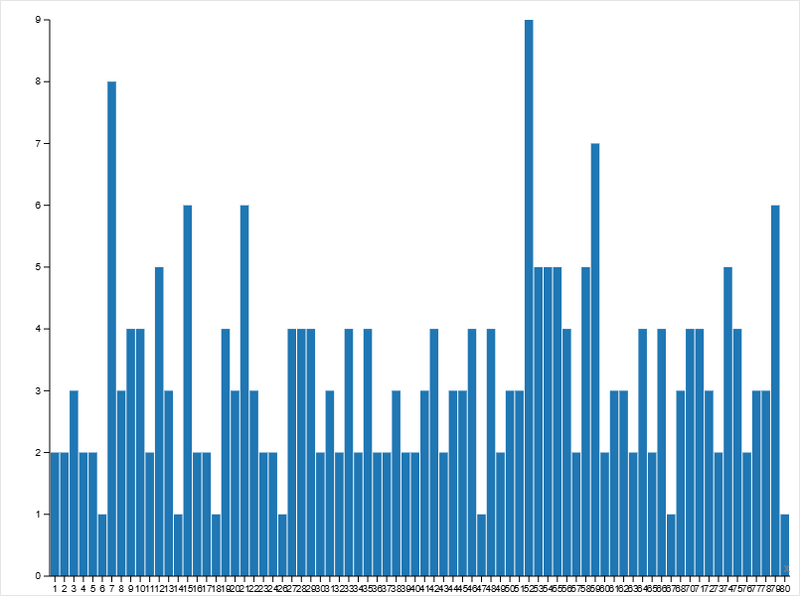
- значения сильно рассеяны по всему диапазону;
- распределение близко к равномерному;
- присутствуют редкие высокие экстремумы.
Mean Values of Batches:

- средние значения крайне разрежены;
- большинство значений встречается 1–2 раза;
- отсутствует выраженный центр распределения.
Широкий sample-space при малом числе messengers усиливает хаотичность. Усреднение практически не снижает разброс, система демонстрирует нестабильные средние значения.
Прогон 3 — большой диапазон, среднее число messengers
- sample-space = 80
- num-messengers = 15
All Values From Messengers:
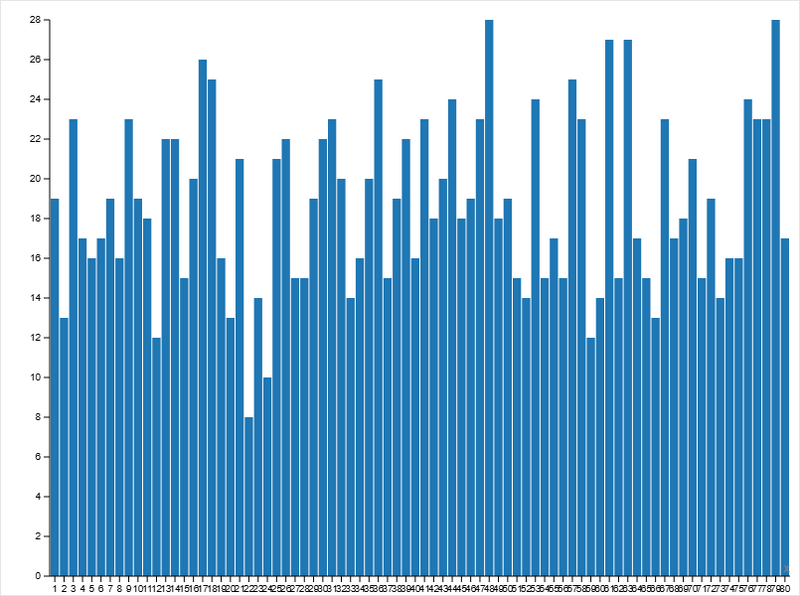
- распределение остаётся широким;
- значения концентрируются в диапазоне 15–25;
- экстремумы присутствуют, но редки.
Mean Values of Batches:
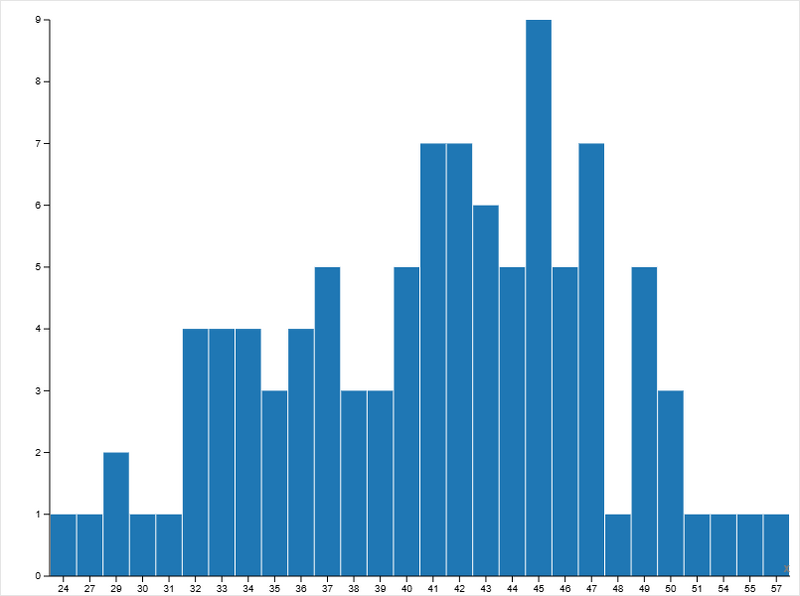
- появляется выраженный центр распределения;
- максимальная частота приходится на средние значения 41–47;
- амплитуда колебаний заметно снижается.
Увеличение числа messengers приводит к частичному сглаживанию случайности. Средние значения становятся более устойчивыми, хотя отдельные выбросы ещё сохраняются. Прогон 4 — большой диапазон, большое число messengers
- sample-space = 80
- num-messengers = 30
All Values From Messengers:
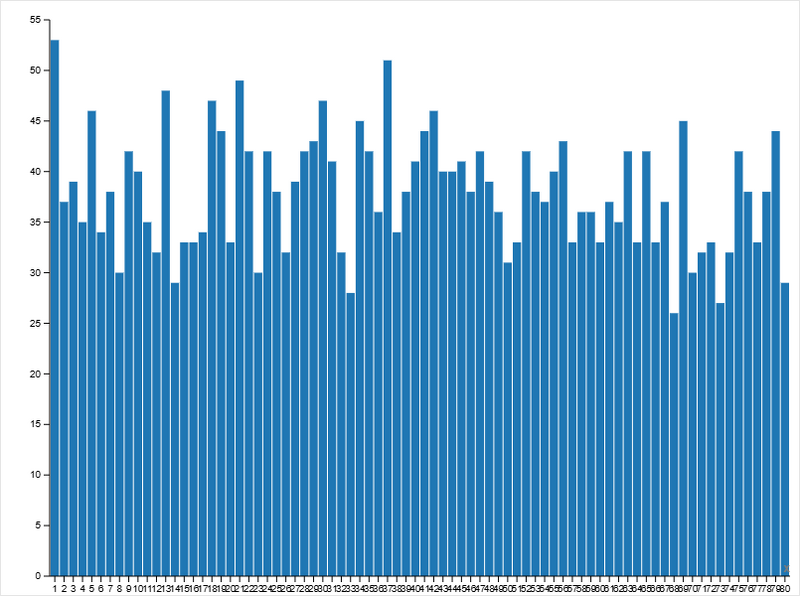
- значения плотно сгруппированы вокруг центральной области (30–45);
- разброс значений снижен по сравнению с предыдущими прогонами;
- экстремальные значения редки.
Mean Values of Batches:
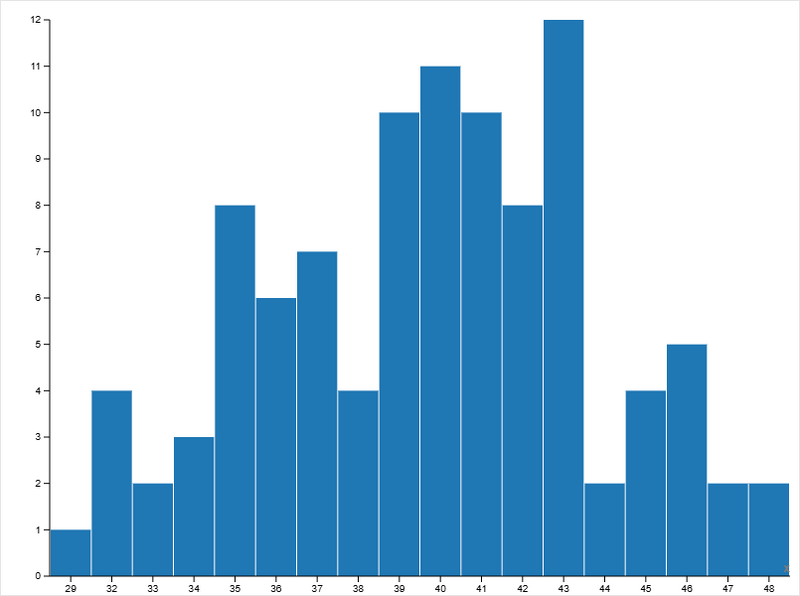
- чётко выраженный пик распределения (40–43);
- большинство средних значений сосредоточено в узком диапазоне;
- минимальная разница между максимумом и минимумом.
При большом числе messengers эффект усреднения становится доминирующим. Система демонстрирует высокую устойчивость, а средние значения слабо зависят от отдельных случайных выборов.
Выводы:
Количество messengers является ключевым фактором устойчивости среднего значения. При увеличении num-messengers разброс средних значений существенно уменьшается. Ширина sample-space усиливает хаотичность системы, но её влияние компенсируется ростом числа messengers. Гистограмма All Values From Messengers отражает исходную случайность, тогда как Mean Values of Batches of Messengers демонстрирует эффект сглаживания. При большом числе messengers система переходит в режим устойчивых средних значений, несмотря на полностью случайную природу индивидуальных действий. Эксперимент наглядно показывает, как из хаотического поведения отдельных агентов возникает предсказуемый коллективный результат.
