Линейный поиск

Линейный, последовательный поиск — алгоритм нахождения заданного значения произвольной функции на некотором отрезке. Данный алгоритм является простейшим алгоритмом поиска и, в отличие, например, от двоичного поиска, не накладывает никаких ограничений на функцию и имеет простейшую реализацию. Поиск значения функции осуществляется простым сравнением очередного рассматриваемого значения (как правило, поиск происходит слева направо, то есть от меньших значений аргумента к большим) и, если значения совпадают (с той или иной точностью), то поиск считается завершённым.

Если отрезок имеет длину N, то найти решение с точностью до [math]\displaystyle{ \epsilon }[/math] можно за время [math]\displaystyle{ N\over\epsilon }[/math]. Т.о. асимптотическая сложность алгоритма — [math]\displaystyle{ O(n) }[/math]. В связи с малой эффективностью по сравнению с другими алгоритмами линейный поиск обычно используют, только если отрезок поиска содержит очень мало элементов, тем не менее, линейный поиск не требует дополнительной памяти или обработки/анализа функции, так что может работать в потоковом режиме при непосредственном получении данных из любого источника. Также линейный поиск часто используется в виде линейных алгоритмов поиска максимума/минимума.

В качестве примера можно рассмотреть поиск значения функции на множестве целых чисел, представленной таблично.

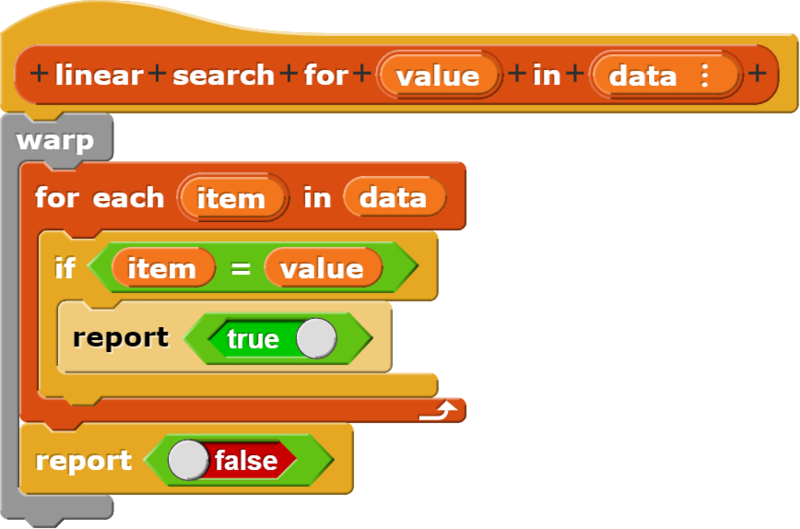
Примеры на Snap!

Есть или нет в списке

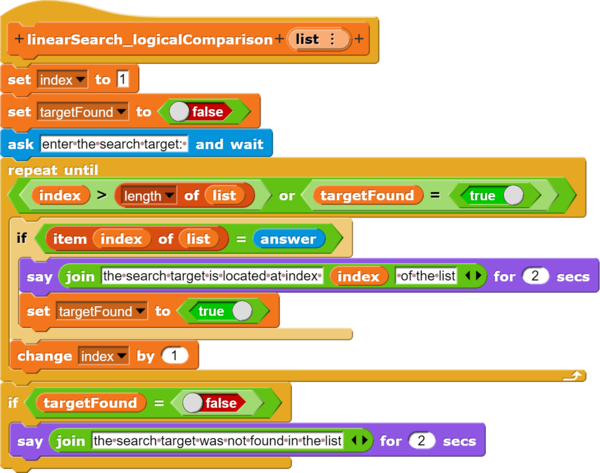
Положение в списке

Пример

Переменные [math]\displaystyle{ L }[/math] и [math]\displaystyle{ R }[/math] содержат, соответственно, левую и правую границы отрезка массива, где находится нужный нам элемент. Исследования начинаются с первого элемента отрезка. Если искомое значение не равно значению функции в данной точке, то осуществляется переход к следующей точке. То есть в результате каждой проверки область поиска уменьшается на один элемент.

int function LinearSearch (Array A, int L, int R, int Key);
begin
  for X = L to R do
    if A[X] = Key then 
      return X
  return -1; // элемент не найден
end;

Пример на Swift

Пример на Swift 3, с "ускоренным" поиском:

 func linearSearch(element: Int, in array: [Int]) -> Int? {
    var array = array
    
    let realLastElement: Int?
    if array.isEmpty {
        return nil
    } else {
        realLastElement = array[array.count - 1]
        array[array.count - 1] = element
    }
    
    var i = 0;
    while array[i] != element {
        i += 1;
    }
    
    let findedElement = array[i];
    if i == array.count - 1 && findedElement != realLastElement {
        return nil
    } else {
        return i
    }
 }

Анализ

Для списка из n элементов лучшим случаем будет тот, при котором искомое значение равно первому элементу списка и требуется только одно сравнение. Худший случай будет тогда, когда значения в списке нет (или оно находится в самом конце списка), в случае чего необходимо n сравнений.

Если искомое значение входит в список k раз и все вхождения равновероятны, то ожидаемое число сравнений

[math]\displaystyle{ \begin{cases} n & k = 0 \\[5pt] \displaystyle\frac{n + 1}{k + 1} & 1 \le k \le n. \end{cases} }[/math]

Например, если искомое значение встречается в списке один раз, и все вхождения равновероятны, то среднее число сравнений равно [math]\displaystyle{ \frac{n + 1}2 }[/math]. Однако, если известно, что оно встречается один раз, то достаточно n — 1 сравнений, и среднее число сравнений будет равняться

[math]\displaystyle{ \displaystyle\frac{(n + 2)(n-1)}{2n} }[/math]

(для n = 2 это число равняется 1, что соответствует одной конструкции if-then-else).

В любом случае вычислительная сложность алгоритма O(n).

Приложения

Обычно линейный поиск очень прост в реализации и применим, если список содержит мало элементов, либо в случае одиночного поиска в неупорядоченном списке.

Если предполагается поиск в одном и том же списке большое число раз, то часто имеет смысл предварительной обработки списка, например, сортировки и последующего использования бинарного поиска, либо построения какой-либо эффективной структуры данных для поиска. Частая модификация списка также может оказывать влияние на выбор дальнейших действий, поскольку делает необходимым процесс перестройки структуры.

---