Персептрон: различия между версиями
Материал из Поле цифровой дидактики
Patarakin (обсуждение | вклад) |
Patarakin (обсуждение | вклад) |
||
| Строка 10: | Строка 10: | ||
Важным свойством любой нейронной сети является способность к обучению. Процесс обучения является процедурой настройки весов и порогов с целью уменьшения разности между желаемыми (целевыми) и получаемыми векторами на выходе. В своей книге Розенблатт пытался классифицировать различные [[алгоритм]]ы обучения перцептрона, называя их системами подкрепления. | Важным свойством любой нейронной сети является способность к обучению. Процесс обучения является процедурой настройки весов и порогов с целью уменьшения разности между желаемыми (целевыми) и получаемыми векторами на выходе. В своей книге Розенблатт пытался классифицировать различные [[алгоритм]]ы обучения перцептрона, называя их системами подкрепления. | ||
Статья и модель [[NetLogo]] http://www.cs.us.es/~fsancho/?e=135 | |||
Версия 16:00, 15 декабря 2022
| Описание | Перцептро́н, или персептрон (англ. perceptron от лат. perceptio — восприятие; нем. Perzeptron) — математическая или компьютерная модель восприятия информации мозгом (кибернетическая модель мозга), предложенная Фрэнком Розенблаттом в 1958 году и впервые реализованная в виде электронной машины «Марк-1» в 1960 году. Перцептрон стал одной из первых моделей нейросетей, а «Марк-1» — первым в мире нейрокомпьютером. |
|---|---|
| Область знаний | NetSci, Информатика |
| Авторы | Розенблатт, Минский, Пейперт |
| Поясняющее видео | |
| Близкие понятия | Нейросеть, Искусственный интеллект, Машинное обучение |
| Среды и средства для освоения понятия |
Алгоритм для выполнения двоичной классификации. Он определяет, относится ли объект к определенной категории (например, является ли животное на рисунке кошкой или нет).
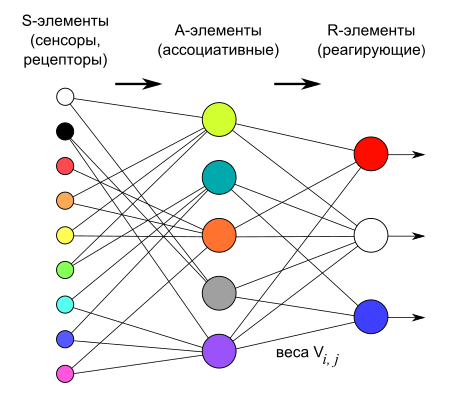
Важным свойством любой нейронной сети является способность к обучению. Процесс обучения является процедурой настройки весов и порогов с целью уменьшения разности между желаемыми (целевыми) и получаемыми векторами на выходе. В своей книге Розенблатт пытался классифицировать различные алгоритмы обучения перцептрона, называя их системами подкрепления.
Статья и модель NetLogo http://www.cs.us.es/~fsancho/?e=135