Использование рекурсивного способа вычисления факториала в Snap!: различия между версиями
LesikAA (обсуждение | вклад) |
LesikAA (обсуждение | вклад) |
||
| Строка 8: | Строка 8: | ||
}} | }} | ||
=== [[ | === [[Основные определения]] === | ||
{| {{prettytable}} | {| {{prettytable}} | ||
|- | |- | ||
!{{Hl2}}| | !{{Hl2}}| Понятие | ||
!{{Hl2}}| Определение | !{{Hl2}}| Определение | ||
|- | |- | ||
| Рекурсия | | Рекурсия | ||
| #ask: Рекурсия | | {{#ask: Рекурсия ?Description}} | ||
|- | |- | ||
| Факториал | | Факториал | ||
Версия 09:53, 18 октября 2024
| Описание | Рекурсивный алгоритм вычисления факториала в Snap! |
|---|---|
| Область знаний | Математика, Информатика |
| Область использования (ISTE) | Computational Thinker |
| Возрастная категория | 14
|
| Поясняющее видео | |
| Близкие рецепту понятия | Рекурсия |
| Среды и средства для приготовления рецепта: | Snap! |
Основные определения
| Понятие | Определение |
|---|---|
| Рекурсия | <ul><li>Ошибка: Часть “Рекурсия ?Description” запроса не была распознана. Результаты могут отличаться от ожидаемых.</li> <!--br--><li>Ошибка: В одном из подзапросов не указано правильного знака условия.</li></ul> |
| Факториал | Факториал числа n — это произведение всех натуральных чисел от 1 до n включительно.
Обозначается факториал числа n следующим образом: n! |
Факториал
Факториал числа n — это произведение всех натуральных чисел от 1 до n включительно. Обозначается факториал числа n следующим образом: n!
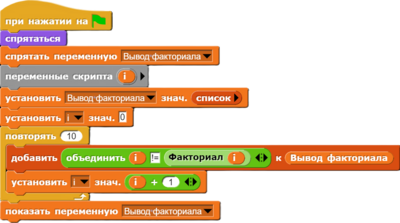
Реализация рекурсивного алгоритма вычисления факториала в Snap!
В представленном примере демонстрируется рекурсивный алгоритм вычисления факториала числа.
В среде программирования Snap! реализована возможность создания пользовательских блоков, представляющих собой функции. В данном случае создан блок с именем "Факториал" типа "Результат", что означает, что он возвращает значение.
После создания блок "Факториал" автоматически добавляется в палитру доступных блоков и может быть использован как при редактировании его определения, так и в других программах.
Эта особенность позволяет реализовывать рекурсию, то есть вызывать блок "Факториал" из самого себя, что необходимо для выполнения рекурсивного алгоритма.