Обсуждение:Как провести регрессионный анализ

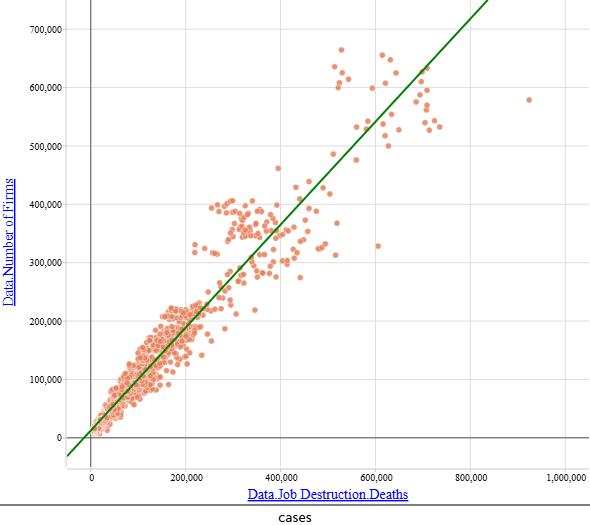
Материал из Поле цифровой дидактики

Дополнение с датасетом про бизнес

Как мы исследовали зависимости из датасета про бизнес

Дополнение с датасетом про кофе

Как проводился регрессионный анализ датасета про кофе:

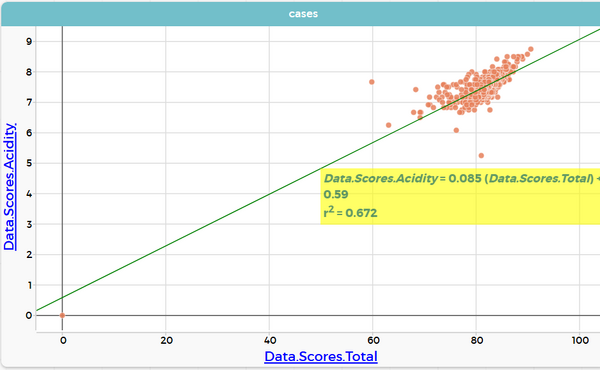
How does (Data.Scores.Acidity) depend on (Data.Scores.Total)? 

 LSRL: Data.Scores.Acidity = 0,08482 (Data.Scores.Total) - NaN 
 N = 989, ρ = 0,8197, r2 = 0,6719

Regression details 

 slope	0,08482	95% CI = [0,08112, 0,08852]
 intercept	0,5867	95% CI = [0,2829, 0,8905]

 testing slope ≠ 0 
 t = 45, P < 0.0001
 df = 987,  α = 0,05, t* = 1,96,


Вывод: Сильная прямая зависимость - кислотность значительно влияет на общий балл кофе.

Ключевые цифры:

Сильная связь: ρ = 0.82 (очень высокая корреляция)

Объясняет 67%: R² = 0.67 - кислотность определяет 67% изменений общего балла

Статзначимо: P < 0.0001 - связь не случайна

Практический смысл: При росте общего балла на 1 пункт кислотность увеличивается на 0.085 балла

Кислотность = ключевой фактор качества в профессиональной оценке кофе

Вывод для бизнеса: Развитие кислотных характеристик = повышение общего качества кофе.

Дополнение с датасетом про миллионеров

Как проводился регрессионный анализ с датасетом про миллионеров:

Гипотеза: Есть ли связь между возрастом и состоянием? Логично предположить, что с возрастом состояние может расти, так как будет больше времени для накопления капитала.

Регрессионный анализ:

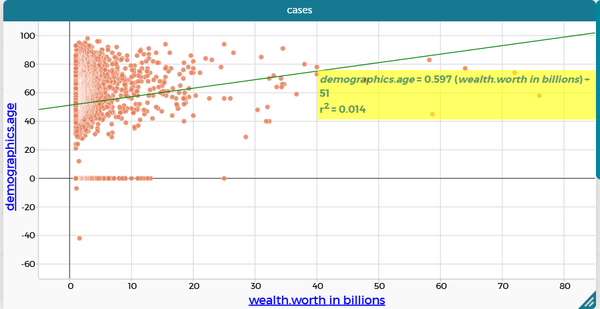
How does (demographics.age) depend on (wealth.worth in billions) ? 

   LSRL: demographics.age = 0,5967 (wealth.worth in billions) - NaN 
   N = 2614, ρ = 0,1199, r2 = 0,01437

Regression details slope 0,5967 95% CI = [0,4071, 0,7864] intercept 51,23 95% CI = [50,06, 52,41] 

testing slope ≠ 0 
   t = 6,17, P < 0.0001
   df = 2612,  α = 0,05, t* = 1,96,

Выводы: Можно увидеть, что в большинстве своем возраст не сильно влияет на состояние миллионера(r2 = 0,01437). Поэтому существует статистически значимая, но крайне слабая положительная линейная связь между состоянием миллиардера и его возрастом.

Дополнение с датасетом про опиоид

Как мы исследовали зависимости из датасета про опиоид https://corgis-edu.github.io/corgis/csv/opioids/

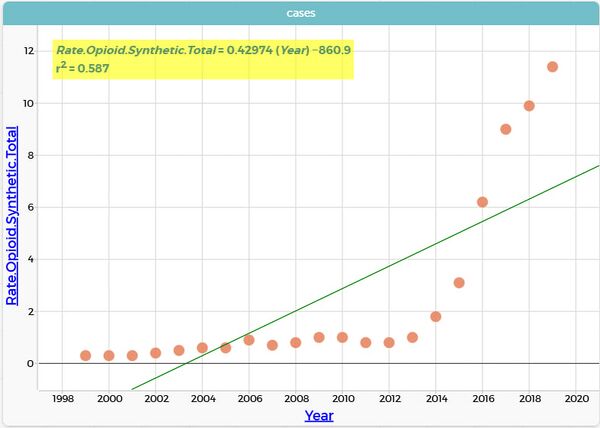
How does (Rate.Opioid.Synthetic.Total) depend on (Year) ? 

   LSRL: Rate.Opioid.Synthetic.Total = 0,4297 (Year) - NaN 
   N = 21, ρ = 0,7664, r2 = 0,5874

Regression details slope 0,4297 95% CI = [0,2568, 0,6027] intercept -860,9 95% CI = [-1208, -513,5] 

testing slope ≠ 0 
   t = 5,2, P < 0.0001
   df = 19,  α = 0,05, t* = 2,09,

Вывод:

  • Сильная положительная корреляция
  • Значительный рост смертности от синтетических опиоидов с течением времени

Дополнение с датасетом по зарплатам выпусников

https://corgis-edu.github.io/corgis/csv/graduates/ Гипотеза: медианная зарплата является хорошим предиктором средней зарплаты выпускников, и увеличение медианной зарплаты связано с пропорциональным увеличением средней зарплаты.

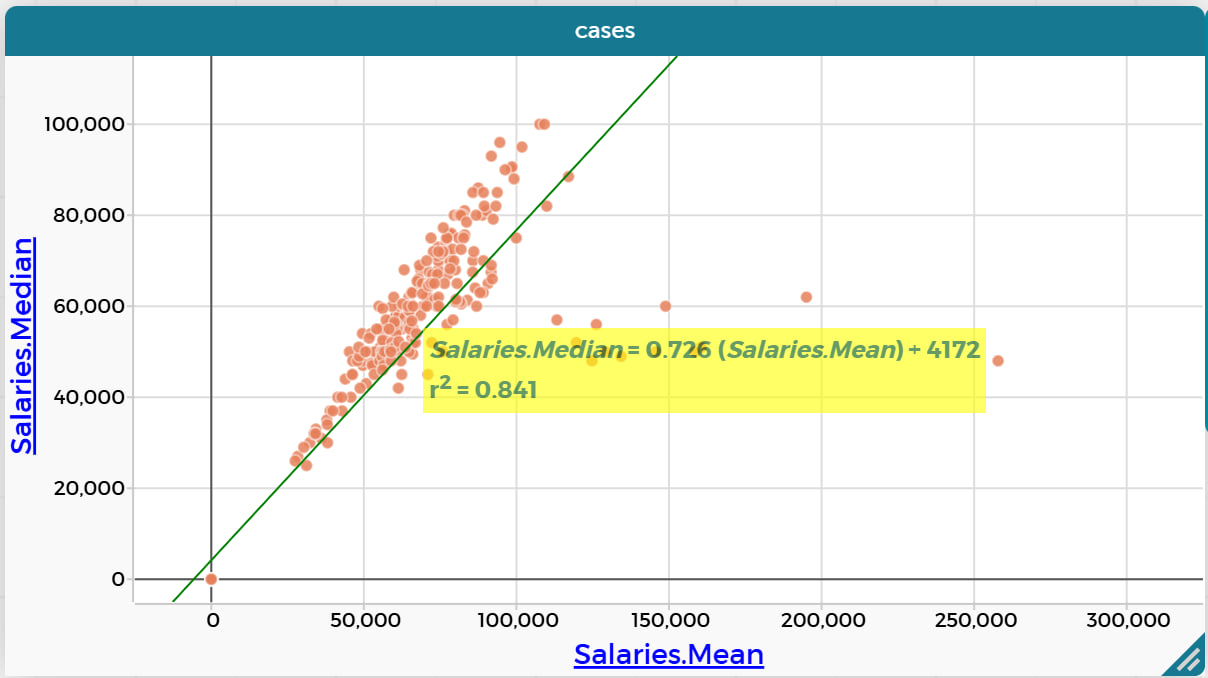500 ptx How does (Salaries.Median) depend on (Salaries.Mean) ? 

   LSRL: Salaries.Median = 0,7259 (Salaries.Mean) + 4172 
   N = 517, ρ = 0,9169, r2 = 0,8407

Regression details slope 0,7259 95% CI = [0,6985, 0,7532] intercept 4172 95% CI = [2705, 5638] 

testing slope ≠ 0 
   t = 52,1, P < 0.0001
   df = 515,  α = 0,05, t* = 1,96,

Выводы: Видно что линейная зависимость действительно есть, однако наблюдается некое отклонение. Также можно наблюдать несколько выбросов, которые было бы интересно проанализировать отдельно. Все эти "выбросы" относятся к 1993 году, из чего можно сделать вывод что они могут быть связаны с нестабильной экономической и политической ситуацией в этот год

Источник — http://digida.mgpu.ru/index.php?title=Обсуждение:Как_провести_регрессионный_анализ&oldid=34131