Двоичный поиск: различия между версиями
Материал из Поле цифровой дидактики
Patarakin (обсуждение | вклад) |
Patarakin (обсуждение | вклад) |
||
| Строка 8: | Строка 8: | ||
# Процесс продолжается до тех пор, пока не будет найден элемент со значением ключа или не станет пустым интервал для поиска. | # Процесс продолжается до тех пор, пока не будет найден элемент со значением ключа или не станет пустым интервал для поиска. | ||
{{#ask: [[Binary search (diagram)]] | format = embedded}} | |||
== Пример реализации на Java == | == Пример реализации на Java == | ||
Версия 14:30, 2 декабря 2022
Двоичный (бинарный) поиск (также известен как метод деления пополам или дихотомия) — классический алгоритм поиска элемента в отсортированном массиве (векторе), использующий дробление массива на половины. Используется в информатике, вычислительной математике и математическом программировании.
Поиск элемента в отсортированном массиве
- Определение значения элемента в середине структуры данных. Полученное значение сравнивается с ключом.
- Если ключ меньше значения середины, то поиск осуществляется в первой половине элементов, иначе — во второй.
- Поиск сводится к тому, что вновь определяется значение серединного элемента в выбранной половине и сравнивается с ключом.
- Процесс продолжается до тех пор, пока не будет найден элемент со значением ключа или не станет пустым интервал для поиска.
Binary search (diagram)
| Описание | 
|
|---|---|
| Область знаний | Информатика |
| Среды для создания диаграммы: | Graphviz, Mermaid |
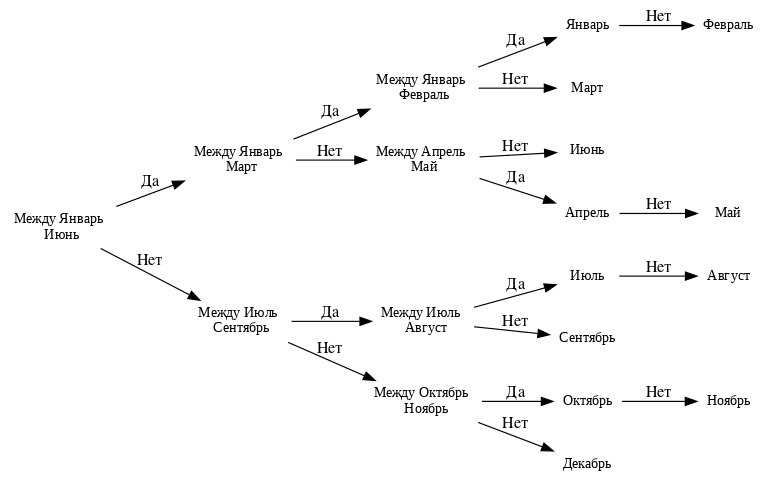
V2

Mermaid
Mermaid - в цифрах
Алгоритм бинарного поиска в интервале 1 - 12
Пример реализации на Java
int binarySearch(int[] arr, int key) {
int low = 0;
int high = arr.length - 1;
while (low <= high) {
int mid = (low + high) >>> 1;
int midVal = arr[mid];
if (midVal < key)
low = mid + 1;
else if (midVal > key)
high = mid - 1;
else
return mid; // key found
}
return -(low + 1); // key not found.
}
Приложения
Практические приложения метода двоичного поиска разнообразны:
- Широкое распространение в информатике применительно к поиску в структурах данных. Например, поиск в массивах данных осуществляется по ключу, присвоенному каждому из элементов массива (в простейшем случае сам элемент является ключом).
- Также его применяют в качестве численного метода для нахождения приближённого решения уравнений (см. Метод бисекции).
- Метод используется для нахождения экстремума целевой функции и в этом случае является методом условной одномерной оптимизации. Когда функция имеет вещественный аргумент, найти решение с точностью до [math]\displaystyle{ \varepsilon }[/math] можно за время [math]\displaystyle{ \log_2 1 / \varepsilon }[/math]. Когда аргумент дискретен, и изначально лежит на отрезке длины N, поиск решения займёт [math]\displaystyle{ 1 + \log_2N }[/math] времени. Наконец, для поиска экстремума, скажем, для определённости минимума, на очередном шаге отбрасывается тот из концов рассматриваемого отрезка, значение в котором максимально.